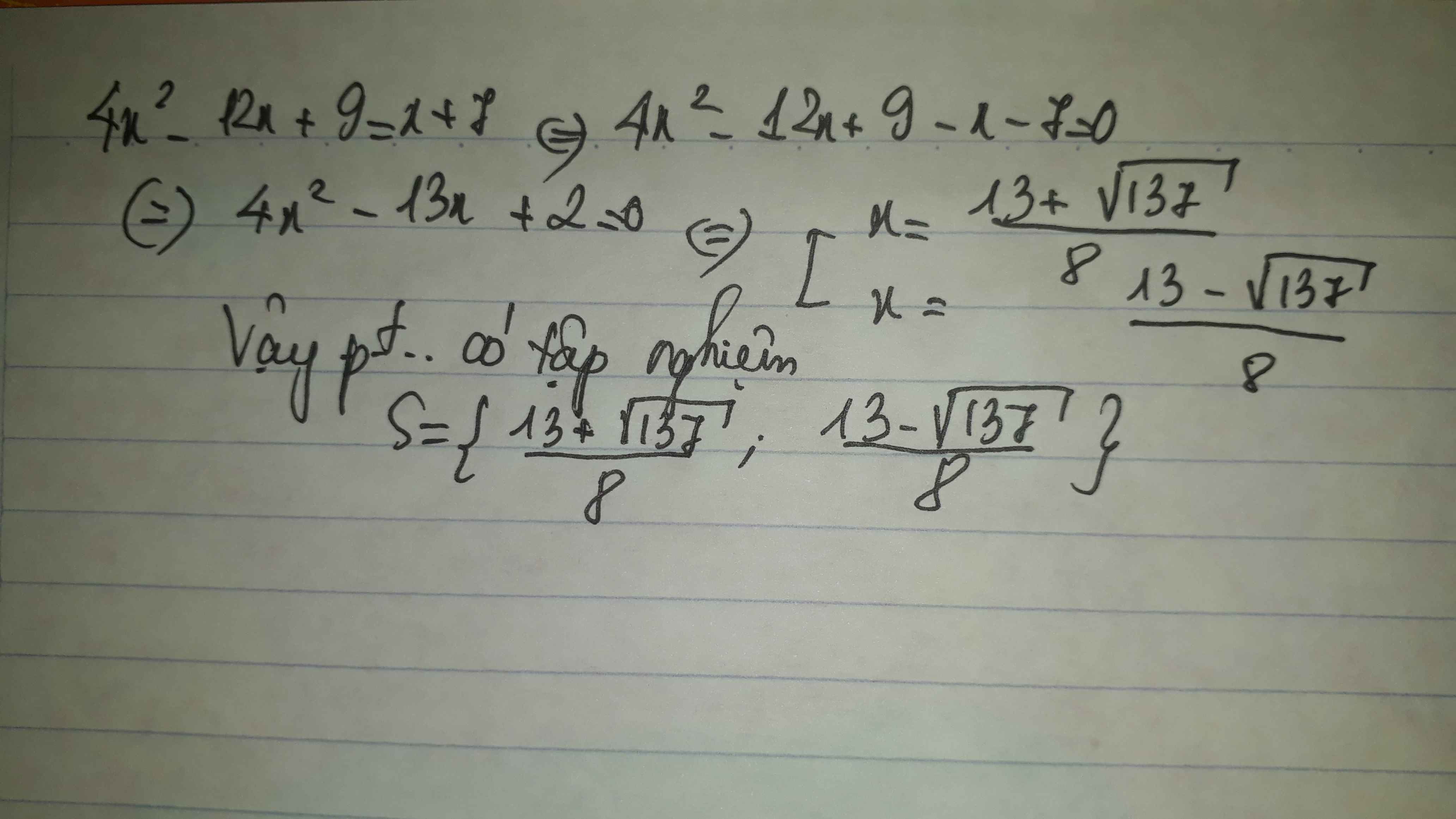20x2-45/4x2+12x +9

Những câu hỏi liên quan
tính G=1+2x2+3x2^2+4x2^3+....+20x2^19
Bạn có thể tham khảo 1 lời giải tương tự ở đây:
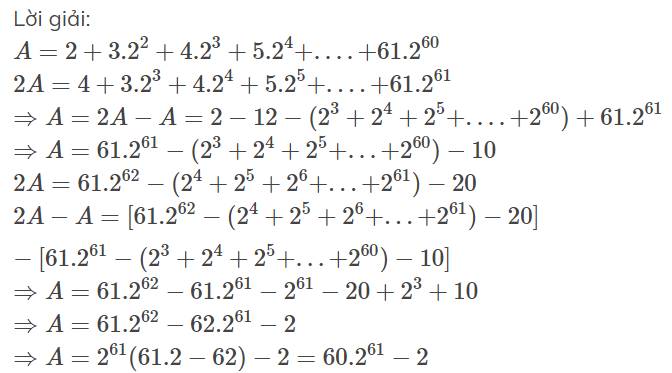
Đúng 0
Bình luận (0)
Hàm số
y
45
+
20
x
2
+
2
x
−
9
có giá trị nhỏ nhất bằng: A. 19 B. 8 C. 15 D. 18
Đọc tiếp
Hàm số y = 45 + 20 x 2 + 2 x − 9 có giá trị nhỏ nhất bằng:
A. 19
B. 8
C. 15
D. 18
Đáp án C
Áp dụng bất đẳng thức C.S ta có:
45 + 20 x 2 = 5 9 + 4 x 2 = 2 2 + 1 2 3 2 + 2 x 2 ≥ 2.3 + 1.2 x = 6 + 2 x
Suy ra y ≥ 6 + 2 x + 2 x − 9 . Áp dụng bất đẳng thức a + b ≥ a + b ta được:
6 + 2 x + 2 x − 9 = 6 + 2 x + 9 − 2 x ≥ 6 + 2 x + 9 − 2 x = 15 ⇒ y ≥ 15
Vậy hàm số y = 45 + 20 x 2 + 2 x − 3 có giá trị nhỏ nhất bằng 9.
Có thể đạo hàm để tìm gtnn.
Đúng 0
Bình luận (0)
giai phuong trinh: 6x+5/12x+9+3x-7/9-12x=4x2+10x-7/16x2-9
4x2-12x+9
Xem thêm câu trả lời
(2x+y)2 -4x2 +12x-9
(2x + y)2 - (2x - 3)2 = (2x + y - 2x + 3)(2x + y + 2x - 3) = (y + 3)(4x + y - 3)
Đúng 1
Bình luận (0)
\(\left(2x+y\right)^2-4x^2+12x-9\)
\(=\left(2x+y\right)^2-\left(2x-3\right)^2\)
\(=\left(2x+y-2x+3\right)\left(2x+y+2x-3\right)\)
\(=\left(y+3\right)\left(4x+y-3\right)\)
Đúng 0
Bình luận (0)
Giải phương trình 4x2-12x+9=x+7
\(4\cdot2-12x+9=x+7\)
\(\Leftrightarrow8-12x+9=x+7\)
\(\Leftrightarrow-12x-x=7-8-9\)
\(\Leftrightarrow-13x=-10\)
\(\Leftrightarrow x=\dfrac{10}{13}\)
Vậy \(x=\dfrac{10}{13}\)
Đúng 0
Bình luận (0)
Ta có: \(4x^2-12x+9=x+7\)
\(\Leftrightarrow4x^2-13x+2=0\)
\(\text{Δ}=\left(-13\right)^2-4\cdot4\cdot2=137\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{13-\sqrt{137}}{8}\\x_2=\dfrac{13+\sqrt{137}}{8}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Đa thức 12x - 9 - 4x2 được phân tích thành:
=(4x2-12x+9)=[(2x)2-2.2x.3+32]=-(2x-3)2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức sau:
\(\sqrt{4x2-4x+1}+\sqrt{4x2-12x+9}\)
Đặt \(C=\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=\left|2x-1\right|+\left|2x-3\right|\)
\(=\left|2x-1\right|+\left|3-2x\right|\)
\(\ge\left|\left(2x-1\right)+\left(3-2x\right)\right|=\left|2\right|=2\)
Vậy \(C_{min}=2\)
Đúng 0
Bình luận (0)
#)Giải :
\(\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=\left|2x-1\right|+\left|2x-3\right|\)
\(=\left|2x-1\right|+\left|3-2x\right|\ge\left|2x-1+3-2x\right|=2\)
Dấu ''='' xảy ra khi x = 1
Đúng 0
Bình luận (0)
\(\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=|2x-1|+|2x-3|\)
\(=|2x-1|+|3-2x|\ge|2x-1+3-2x|=2\)
Dấu"=" xảy ra \(\Leftrightarrow\left(2x-1\right)\left(3-2x\right)\ge0\Leftrightarrow\frac{1}{2}\le x\le\frac{3}{2}\)
Chỉ là góp ý:V
Đúng 0
Bình luận (1)
Viết các biểu thức sau dưới dạng bình phương của một tổng
a) x2 + 3x +1
b) x2 + y2 + 2xy
c) 9x2 +12x +4
d) -4x2 - 9 - 12x
a) Sửa đề: \(x^2+3x+1\rightarrow x^2+2x+1\)
\(x^2+2x+1=\left(x+1\right)^2\)
b) \(x^2+y^2+2xy=\left(x+y\right)^2\)
c) \(9x^2+12x+4=\left(3x+2\right)^2\)
d) \(-4x^2-9-12x=-\left(4x^2+12x+9\right)=-\left(2x+3\right)^2\)
Đúng 1
Bình luận (0)
Thực hiện các phép tính sau:a)
P
(
4
x
2
−
1
)
1
2
x
−
1
−
1
2
x
+
1
−...
Đọc tiếp
Thực hiện các phép tính sau:
a) P = ( 4 x 2 − 1 ) 1 2 x − 1 − 1 2 x + 1 − 1 với x ≠ ± 1 2 ;
b) Q = 3 x + 3 − 9 x 2 + 6 x + 9 : 3 x 2 − 9 + 1 3 − x với x ≠ 0 và x ≠ ± 3
a) Ta có P = ( 4 x 2 − 1 ) ( 2 x + 1 ) − ( 2 x − 1 ) − ( 4 x 2 − 1 ) ( 2 x + 1 ) ( 2 x − 1 ) = 3 − 4 x 2
b) Ta có Q = 3 x ( x + 3 ) . ( x + 3 ) ( x − 3 ) − x = 9 − 3 x x + 3
Đúng 0
Bình luận (0)