câu f thôi ạ

Làm giúp em câu F thôi ạ
giúp mik câu d,e,f thôi ạ
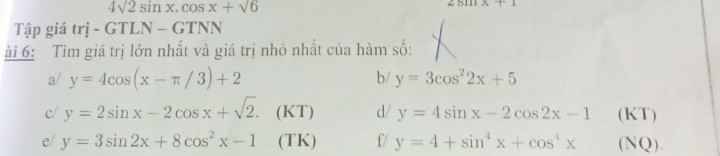
d) \(y=4sinx-2cos2x-1\)
\(=4sinx-2\left(1-2sin^2x\right)-1\)
\(=4sin^2x+4sinx-3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=f\left(t\right)=4t^2+4t-3\) \(\Leftrightarrow f'\left(t\right)=8t+4\)
\(f'\left(t\right)=0\Leftrightarrow t=-\dfrac{1}{2}\)
Vẽ BBT với \(t\in\left[-1;1\right]\) ta được
\(minf\left(t\right)=miny=-4\Leftrightarrow t=-\dfrac{1}{2}\)\(\Leftrightarrow sinx=-\dfrac{1}{2}\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) ( k thuộc Z)
\(maxf\left(t\right)=miny=5\Leftrightarrow t=1\)\(\Leftrightarrow sinx=1\) \(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\) ( k thuộc Z)
Vậy...
e) \(y=3sin2x+8cos^2x-1\)
\(=3sin2x+4\left(2cos^2x-1\right)+3\)
\(=3sin2x+4cos2x+3\)
\(=5\left(\dfrac{3}{5}sin2x+\dfrac{4}{5}cos2x\right)+3\)
Đặt \(cosu=\dfrac{3}{5}\Leftrightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sin2x.cosu+cos2x.sinu\right)+3=5.sin\left(2x+u\right)+3\)
Có \(-1\le sin\left(2x+u\right)\le1\) \(\Leftrightarrow-2\le y\le8\)
\(maxy=8\Leftrightarrow sin\left(2x+u\right)=1\) \(\Leftrightarrow2x+u=\dfrac{\pi}{2}+k2\pi\) \(\Leftrightarrow x=-\dfrac{u}{2}+\dfrac{\pi}{4}+k\pi\)\(\Leftrightarrow x=-\dfrac{1}{2}.arccos\dfrac{3}{5}+\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
\(miny=-2\Leftrightarrow sin\left(2x+u\right)=-1\)\(\Leftrightarrow x=-\dfrac{1}{2}.\dfrac{arccos3}{5}-\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
Vậy...
f)\(y=4+sin^4x+cos^4x\)
\(=4+\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=4+1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=5-\dfrac{1}{2}.\left(sin2x\right)^2\)
\(\left(sin2x\right)^2\in\left[0;1\right]\Leftrightarrow y\in\left[\dfrac{9}{2};\dfrac{11}{2}\right]\)
\(maxy=\dfrac{11}{2}\Leftrightarrow sin2x=0\Leftrightarrow2x=k\pi\Leftrightarrow x=\dfrac{k\pi}{2}\) ( k thuộc Z )
\(miny=\dfrac{9}{2}\Leftrightarrow\left(sin2x\right)^2=1\)\(\Leftrightarrow cos2x=0\)\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\) ( k thuộc Z )
Vậy...
Làm giúp em câu F và G thôi ạ
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có KA là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AEKF có
\(\widehat{FAE}=\widehat{AFK}=\widehat{AEK}=90^0\)
Do đó: AEKF là hình chữ nhật
Suy ra: \(AK=EF\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(EF^2=AE\cdot AB\)
c: Ta có: \(AE\cdot AB+AF\cdot AC+KB\cdot KC\)
\(=AH^2+AH^2+AH^2\)
\(=3\cdot EF^2\)
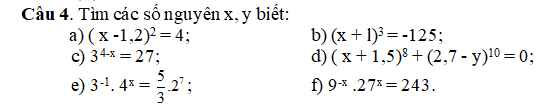 giúp mik câu c d e f thôi ạ :))
giúp mik câu c d e f thôi ạ :))
a: \(\left(x-1.2\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1.2=2\\x-1.2=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3.2\\x=-0.8\end{matrix}\right.\)
b: Ta có: \(\left(x+1\right)^3=-125\)
\(\Leftrightarrow x+1=-5\)
hay x=-6
giúp mik vs ạ!!!
câu e, f, g thôi nha

\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)
e)\(\left(x-2-4\right)\left(x-2+4\right)=\left(x-6\right)\left(x+2\right)\)
f)\(x^2-5x-14=x^2-2.\dfrac{5}{2}x+\dfrac{25}{2}+\dfrac{3}{2}=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{2}\)
e: Ta có: \(\left(x-2\right)^2-16=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
f: Ta có: \(x^2-5x-14=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\)
Giúp em bai 1 với câu e với f thôi ạ
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
c)Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Làm bài c thôi ạ mấy câu còn lại nháp thôi ạ.
MN GIÚP MIK CÂU Ý 3 THÔI Ạ
MIK CHỈ CẦN Ý 3 THÔI Ạ
KO CẦN Ý 1,2 Ạ

giúp câu 2 thôi ạ lý luận thôi nha
Bài 2:
\(a,P=8ab^2+7ab^2=15ab^2\\ Q=\dfrac{3}{2}a^2b-\dfrac{5}{8}a^2b-\dfrac{7}{8}a^2b=0\)
Vì \(ab^2\ne0\Rightarrow\) P không đồng dạng với Q
b, ảnh nhỏ quá ko nhìn thấy
Bài 2:
b: \(A=-8mn+\dfrac{1}{5}mn=-\dfrac{39}{5}mn\)
\(B=4mn-\dfrac{3}{2}mn=\dfrac{5}{2}mn\)
Do đó: A đồng dạng với B