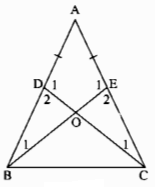
a) Xét ∆BEA và ∆CDA, ta có:

BA = CA (gt)

\(\widehat{A}\)chung

AE = AD (gt)

Suy ra: ∆BEA = ∆CDA (c.g.c)

Vậy BE = CD (hai cạnh tương ứng)

b) ∆BEA = ∆CDA (chứng minh trên)

\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)

\(\widehat{\text{E1}}+\widehat{\text{E2}}\) (hai góc kề bù)

\(\widehat{\text{D1}}+\widehat{\text{D2}}\) (hai góc kề bù)

Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)

AB = AC (gt)

AE + EC = AD + DB mà AE = AD (gt) => EC = DB

Xét ∆ODB và ∆OCE, ta có:

\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)

DB = EC (chứng minh trên)

\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)

Suy ra: ∆ODB = ∆OEC (g.c.g)

Nguyễn Thuỳ Linh               Hình như bài này t lm cho c r mà nhỉ

( Hình tự vẽ )

a) +) Xét \(\Delta\)ABE và \(\Delta\)ACD có

AB = AC ( gt)

\(\widehat{BAC}\) : góc chung

AE = AD ( gt)

=> \(\Delta\)ABE = \(\Delta\)ACD  (c-g-c)

b) Theo câu a ta có  \(\Delta\)ABE = \(\Delta\)ACD 

=> BE = CD  ( 2 cạnh tương ứng )

c) +) Xét  \(\Delta\) ABC cân tại A 

=> \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)  (1)    ( tính chất tam giác cân )

+) Xét \(\Delta\)AED có AE = AD  ( gt)

=> \(\Delta\)AED cân tại A

=> \(\widehat{AED}=\frac{180^o-\widehat{A}}{2}\)  (2)    ( tính chất tam giác cân )

Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{AED}\)

Mà 2 góc này ở vị trí đồng vị

=> ED // BC

@@ Hc tốt

Takigawa Miu_

a: Xét ΔABE và ΔACD có 

AB=AC

\(\widehat{A}\) chung

AE=AD

Do đó: ΔABE=ΔACD

Xét ΔDBC và ΔECB có

DB=EC

BC chung

DC=EB

Do đó: ΔDBC=ΔECB

Xét ΔKBD và ΔKCE có 

\(\widehat{KBD}=\widehat{KCE}\)

BD=CE

\(\widehat{KDB}=\widehat{KEC}\)

Do đó:ΔKBD=ΔKCE

a/ Xét tam giác BCD và tam giác BCE có

-góc B = góc C

-BD = EC

-BC: cạnh chung

=> tam giác BCD = tam giác BCE (cạnh góc cạnh)

=> BE=CD (2 cạnh tương ứng)

b/ Xét tam giác KBD và tam giác KCE có

-Góc BKD = góc CKE (đối đỉnh)

-BD=CE

-KB=KC

=> tam giác KBD = tam giác KCE

giúp m v :(

a: Xét ΔABC có AD/AB=AE/AC

nên DE//BC

b: Xét ΔABE và ΔACD có

AB=AC

góc A chung

AE=AD

=>ΔABE=ΔACD

c: Xét ΔIDB và ΔIEC có

góc IDB=góc IEC

DB=EC

góc IBD=góc ICE

=>ΔIDB=ΔIEC

d: Xét ΔABI và ΔACI có

AB=AC

BI=CI

AI chung

=>ΔABI=ΔACI

=>góc BAI=góc CAI

=>AI là phân giác của góc BAC

Giúp mk đi

a: Xét ΔABF và ΔACE có 

AB=AC

\(\widehat{A}\) chung

AF=AE

Do đó: ΔABF=ΔACE

a) Xét \(\Delta ABE\) và \(\Delta ACD\)

có: + AE=AD(gt)

       +A: là góc chung

        +AB=AC(do \(\Delta ABC\) cân tại A)

Vậy \(\Delta ABE\)=\(\Delta ACD\) (c.g.c)

=> BE=CD( 2 cạnh tương ứng)

b) Vì \(\Delta ABE\) =\(\Delta ACD\) (cmt)

nên: góc ABE=góc ACD( 2 góc tương ứng)

c) .\(\Delta KBC\) cân tại K

. Ta có: góc B = \(B_1+B_2\)

                     C=\(C_1=C_2\)

                     B=C(gt);\(B_1=C_1\) (cmt)

=> \(B_2=C_2\)

Do đó \(\Delta KBC\) cân tại K

có bạn nào giải được bài này ko giúp mk với  huhuhu

Bạn cứ từ từ, các bạn tranh nhau đăng câu hỏi mà có mỗi mình giúp các bạn môn Toán. Nếu bạn muốn trả lời nhanh thì kêu mấy đứa đăng ảnh kia đừng đăng câu hỏi nữa để mình làm cho dễ

a, Xét

có: AB=AC

^A là góc chung

AD=AE

==>

^K1=^K2 (đđ)

BD=CE( AB=AC và AD=AE)

KD=KE

==>

AKC

có AK cạnh chung

KB=KC

AB=AC

=>AKC (c-c-c)

=> ^BAK= ^CAK mà AK là cạnh chung

=> AK là tia phân giác của góc BAC