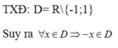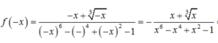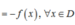Chọn D

Vậy hàm số đa cho là lẻ

Chọn B.

Tập xác định D = R; ∀ x ∈ D có -x ∈ D và

f ( - x )   =   3 . ( - x ) 2   -   1   =   3 x 2   -   1   =   f ( x )

    Vậy hàm số đã cho là hàm số chẵn.

\(f'\left(x\right)=4x^3\Rightarrow g\left(x\right)=4x^3-3x^2-6x+1\)

\(g'\left(x\right)=12x^2-6x-6=0\Rightarrow\left[{}\begin{matrix}x_2=-\dfrac{1}{2}\\x_1=1\end{matrix}\right.\)

\(\Rightarrow g\left(-\dfrac{1}{2}\right).g\left(1\right)=\dfrac{11}{4}.\left(-4\right)=-11\)

\(y'=\left(6x^5-6\right)f'\left(x^6-3x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^6-3x^2\right)=0\end{matrix}\right.\) trong đó \(x=1\) bội lẻ

\(f'\left(x\right)=0\) có các nghiệm \(x=-2;0;2;a;6\)

\(\Rightarrow f'\left(x^6-3x^2\right)=0\Leftrightarrow\) 5 trường hợp:

\(x^6-3x^2=-2\) \(\Leftrightarrow\left(x+1\right)^2\left(x-1\right)^2\left(x^2+2\right)=0\) có 2 nghiệm \(x=-1\) (bội chẵn) và \(x=1\) (bội chẵn)

.... làm tương tự

Riêng với \(x^6-3x^2=a\) thì dựa trên BBT của \(y=x^6-3x^2\) ta thấy pt này có 2 nghiệm đều bội lẻ khi \(4< a< 6\)

Đếm số nghiệm bội lẻ là được

a, ĐK: \(x\ne\dfrac{k\pi}{2}\)

\(y=f\left(x\right)=\dfrac{1}{tanx}\)

\(f\left(-x\right)=\dfrac{1}{tan\left(-x\right)}=-\dfrac{1}{tanx}=-f\left(x\right)\Rightarrow\) Là hàm số lẻ.

c, \(y=f\left(x\right)=sin^2x+2cosx-3\)

\(f\left(-x\right)=sin^2\left(-x\right)+2cos\left(-x\right)-3\)

\(=\left(-sinx\right)^2+2cosx-3\)

\(=sin^2x+2cosx-3=f\left(x\right)\)

\(\Rightarrow\) Là hàm số chẵn.

b, Xem lại đề.

y = f(x) = 3x2 – 2

TXĐ:D = R ⇒ x ∈ D thì-x ∈ D

Ta có: f(-x) = 3(-x)2 – 2 = 3x2 – 2 = f(x)

Vậy hàm số y = f(x) = 3x2 – 2 là hàm số chẵn

Chọn D.

Ta có: f’(x) = -4x³ + 12x² – 6x + 2.

Nên f’(-1) = 24.