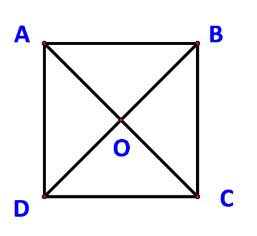
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA}  + \overrightarrow {DC}  = \overrightarrow {DB} \)

\( \Rightarrow \;|\overrightarrow {DA}  + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)

b) Ta có: \(\overrightarrow {AD}  + \overrightarrow {DB}  = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB} \)

\( \Rightarrow \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)

c) Ta có: \(\overrightarrow {DO}  = \overrightarrow {OB} \)

\( \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {DO}  = \overrightarrow {DO}  + \overrightarrow {OA}  = \overrightarrow {DA} \)

\( \Rightarrow \left| {\overrightarrow {OA}  + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)

1: \(=\left|\overrightarrow{CO}-\overrightarrow{CB}\right|=BO=\dfrac{a\sqrt{2}}{2}\)

a: AB=BC=CD=DA=6a

\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)

\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)

\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)

\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)

\(=6a\sqrt{5}\)

b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)

\(=36a^2\)

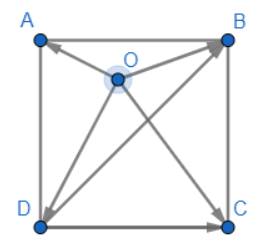
Ta có: \(AB = BC = CD = DA = 1;\)

            \(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

a) \(\overrightarrow a  = \overrightarrow {OB}  - \overrightarrow {OD}  = \overrightarrow {OB}  + \overrightarrow {DO}  = \left( {\overrightarrow {DO}  + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)

\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)

b)  \(\overrightarrow b = \left( {\overrightarrow {OC}  - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB}  - \overrightarrow {DC} } \right)\)

   \( = \left( {\overrightarrow {OC}  + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB}  + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO}  + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD}  + \overrightarrow {DB} } \right)\)

   \( = \overrightarrow {AC}  + \overrightarrow {CB}  = \overrightarrow {AB} \)

\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)

Chú ý khi giải:

Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại

Bạn tham khảo lời giải tại đây:

Câu hỏi của Thư Nguyễn - Toán lớp 10 | Học trực tuyến

Lời giải:

Gọi $M,N$ lần lượt là trung điểm $AB, CD$. Ta có:

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OM}+\overrightarrow{MA}+\overrightarrow{OM}+\overrightarrow{MB}+\overrightarrow{ON}+\overrightarrow{NC}+\overrightarrow{ON}+\overrightarrow{ND}$

$=2\overrightarrow{OM}+2\overrightarrow{ON}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{OM}=-\overrightarrow{ON}$ nên $O$ là trung điểm $MN$

Tam giác $OAB$ cân tại $O$ có $OM$ là trung tuyến đồng thời là đường cao

$\Rightarrow OM\perp AB$. Hoàn toàn tương tự $ON\perp CD$

Mà $O,M,N$ thẳng hàng nên $AB\parallel CD(1)$

Tương tự, đặt $P,Q$ là trung điểm $AD, BC$ ta có:

$AD\paralle BC(2)$

Từ $(1);(2)\Rightarrow ABCD$ là hình bình hành.

$MN$ là đường trung bình của hbh $ABCD$ nên $MN\parallel BC$. Mà ở trên ta chỉ ra $OM\perp AB; O,N,M$ thẳng hàng nên $AB\perp BC$

Hình bình hành $ABCD$ có 2 cạnh kề vuông góc nên là hình chữ nhật.

ABCD là hình vuông

\(\Rightarrow\Delta ABD\&\Delta ACD\) là tam vuông cân

\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|.\sqrt[]{2}\\\left|\overrightarrow{BD}\right|=\left|\overrightarrow{AB}\right|.\sqrt[]{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\\\left|\overrightarrow{BD}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\end{matrix}\right.\)

\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.\left|\overrightarrow{AC}\right|\)  (O là trung điểm AC)

\(\Rightarrow\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.1=\dfrac{1}{2}\)

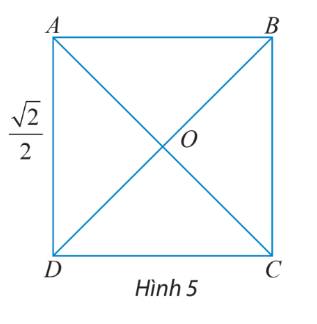
Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}}  = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}  = 1\)

\(OA = \frac{1}{2}AC = \frac{1}{2}\)

Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\)