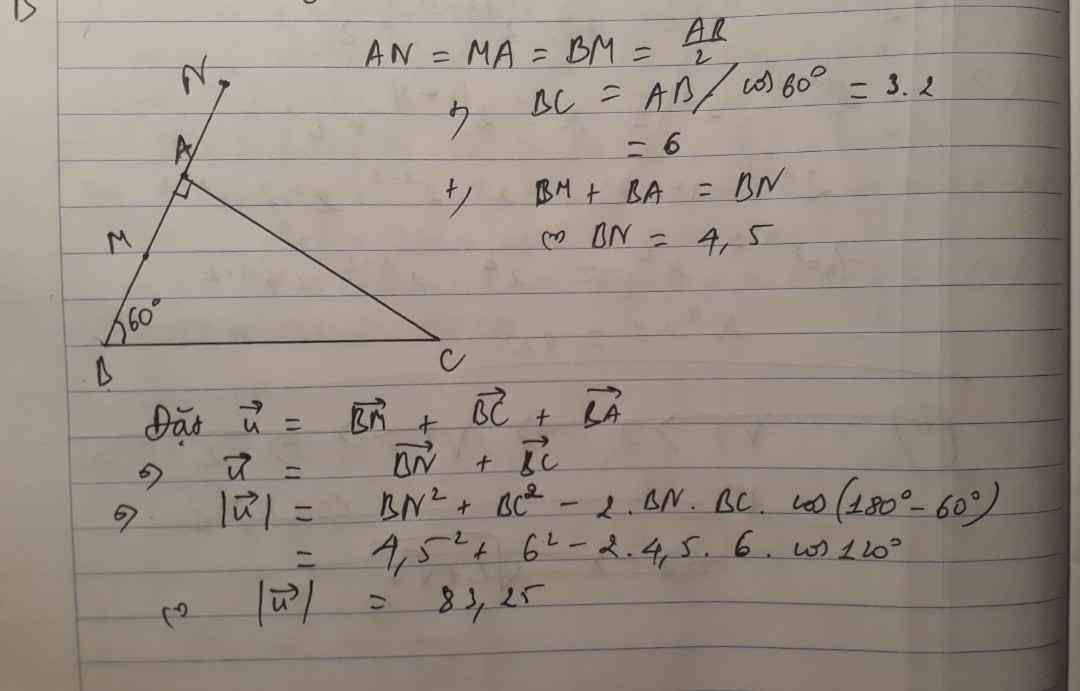Cho tam giác ABC vuông cân tại A có AB=a. Tính |vecto AB+ vecto AC|

Những câu hỏi liên quan
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
a: Ta có: M là trung điểm của BC
=>\(\overrightarrow{MB}=\overrightarrow{CM}\)
\(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}\)
\(\overrightarrow{AC}+\overrightarrow{MB}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AM}\)
Do đó: \(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
b:
ΔABC cân tại A
=>\(\hat{ABC}=\hat{ACB}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-120^0}{2}=30^0\)
ΔABC cân tại A
mà AM là đường trung tuyến
nên AM⊥BC
Xét ΔAMB vuông tại M có \(\sin B=\frac{AM}{AB}\)
=>\(\frac{AM}{6}=\sin30=\frac12\)
=>AM=3(cm)
\(\left|\overrightarrow{AB}-\overrightarrow{CM}\right|=\left|\overrightarrow{AB}+\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{AB}+\overrightarrow{BM}\right|=\left|\overrightarrow{AM}\right|=AM\) =3(cm)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Sửa đề: Chứng minh \(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
\(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}\)
\(\overrightarrow{AC}-\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AC}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AC}-\overrightarrow{MC}\)
=>\(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, AB= a Tínhđộ dài vecto \(3AB\rightarrow\)+→AC
\(\left|3\overrightarrow{AB}+\overrightarrow{AC}\right|=4a\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=3 góc B=60° .Gọi M là điểm thỏa vecto MA + vecto MB= vecto 0. Tính độ dài vecto BM + vecto BC + vecto BA
Cho tam giác ABC vuông cân tại C, AB = 2a và I là trung điểm của BC. Tính |vecto AI - vecto IB|
Tam giác vuông cân tại C \(\Rightarrow AC=\dfrac{AB}{\sqrt{2}}=a\sqrt{2}\)
Do I là trung điểm BC \(\Rightarrow\overrightarrow{IC}=-\overrightarrow{IB}\)
Vậy:
\(\left|\overrightarrow{AI}-\overrightarrow{IB}\right|=\left|\overrightarrow{AI}+\overrightarrow{IC}\right|=\left|\overrightarrow{AC}\right|=AC=a\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
: Cho tam giác ABC vuông tại A có BC cm = 4 . Độ dài của vecto
AB+ AC = bn
Trong tọa độ Oxy, Cho tam giác ABC với A(2:-3),B(4:7),C(-3:2) a) tìm tọa độ vecto AB, vecto AC, vecto BC b) tính tích vô hướng của vecto AB.BC và vecto AB.AC c) tính góc tạo bởi các vecto AB và AC, AB vad BC d) tính chu vi của tam giác ABC
\(a,\overrightarrow{AB}=\left(2;10\right)\)
\(\overrightarrow{AC}=\left(-5;5\right)\)
\(\overrightarrow{BC}=\left(-7;-5\right)\)
\(b,\) Thiếu dữ kiện
\(c,Cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\dfrac{\left|2\left(-5\right)+10.5\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-5\right)^2+5^2}}=\dfrac{2\sqrt{13}}{13}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{AC}\right)=56^o18'\)
\(Cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\dfrac{\left|2\left(-7\right)+10\left(-5\right)\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-7\right)^2+\left(-5\right)^2}}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=43^o9'\)
Đúng 0
Bình luận (0)
cho tam giác ABC có A(-1;3), B(2;4), C(0;1) tính vecto AB.AC tính cos vecto (AB,AC) tính chu vi tam giác ABC
Cho tam giác ABC vuông tại A có AB = 3a, AC = 4a. Khi đó độ dài vecto BC là
Lời giải:
$|\overrightarrow{BC}|=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$ theo định lý Pitago.
Đúng 2
Bình luận (0)