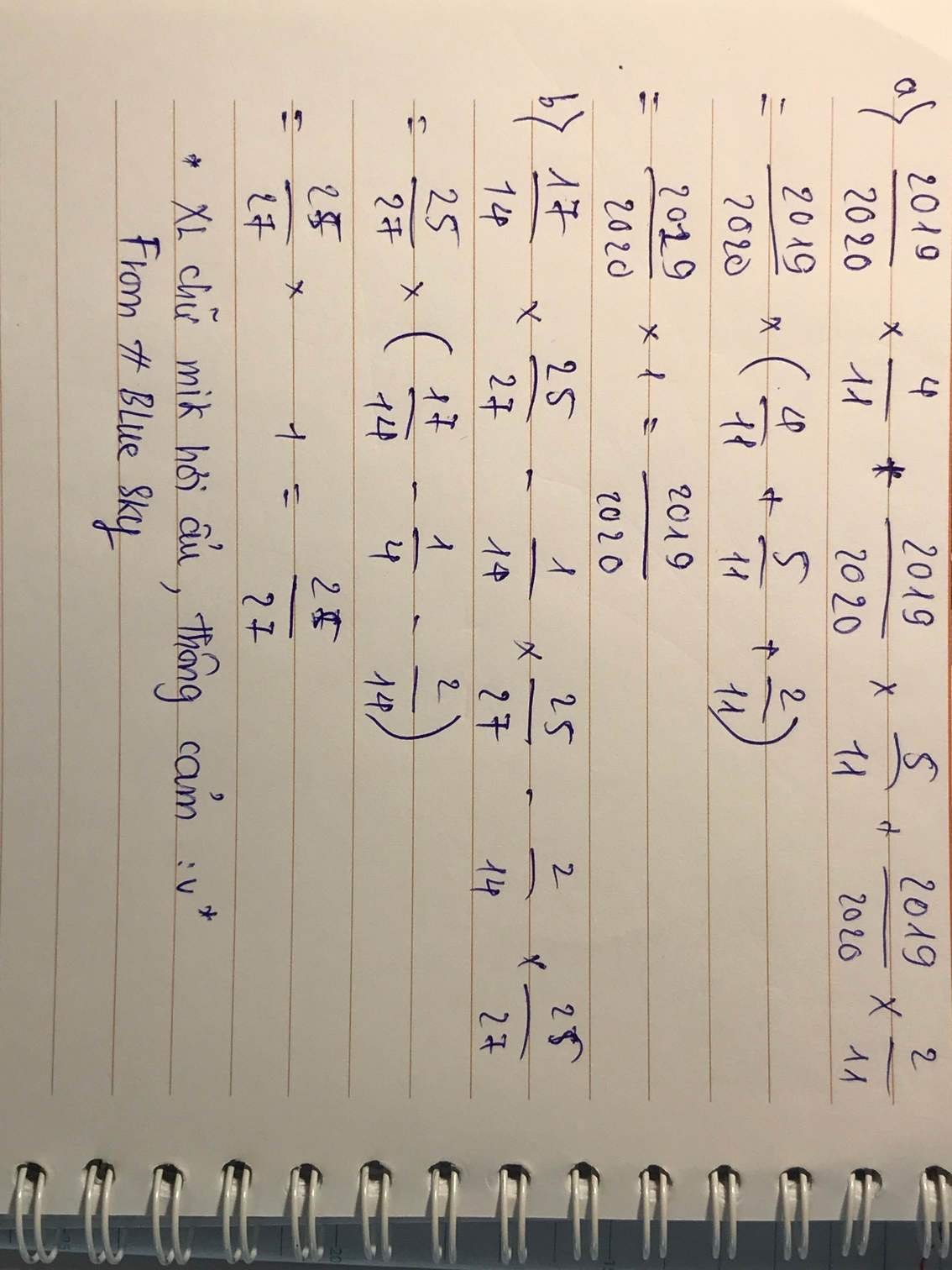x+1/10+x+101+x+1/375=x+1/2019+x+1/2020

Những câu hỏi liên quan
Nếu 1/3 + 1/6 +1/10 + ...... + 1/x.(x+1) : 2 = 2019/2021
A.x = 2019/2020 B. x = 2019 C. x = 2020 D. x = 2021
Xem thêm câu trả lời
2019 x 2020 - 1/ 2019 x 2020 và 2020 x 2021 - 1/ 2020 x 2021
so sánh phân số
Bài 1: thực hiện phép tính
a)1/1×2+1/2×3+1/3×4+...+1/2019×2020
b)1/1×3+1/3×5+1/5×7+...+1/2017×2019
c)3^0+3^1+3^2+...+3^100
d)1/2+1/2^2+1/2^3+...+1/2^2019
Bài2:tìm x
a)|x-2|+|x2 -4=0
b)x+1/2.x-25%.x=10
c)2+4+6+8+...+2x=210
d)1/5×8+1/8×11+1/11×14+...+1/x(x+3)=101/1504
Chú ý: dấu chấm ở câu b)bài 2 là dấu nhân
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2019.2020}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2019}-\frac{1}{2020}\)
\(A=1-\frac{1}{2020}\)
\(A=\frac{2019}{2020}\)
Đúng 0
Bình luận (0)
\(B=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{2017.2019}\)
\(2B=\frac{2}{1.3}+\frac{2}{3.5}=\frac{2}{5.7}+...+\frac{2}{2017.2019}\)
\(2B=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}=\frac{1}{5}-\frac{1}{7}+...+\frac{1}{2017}-\frac{1}{2019}\)
\(2B=1-\frac{1}{2019}\)
\(2B=\frac{2018}{2019}\)
\(B=\frac{2018}{2019}:2=\frac{1009}{2019}\)
Đúng 0
Bình luận (0)
\(C=3^0+3^1+3^2+...+3^{100}\)
\(3C=3^1+3^2+3^3+...+3^{101}\)
\(3C-C=\left(3^1+3^2+3^3+...+3^{101}\right)-\left(1+3^1+3^2+...+3^{100}\right)\)
\(2C=3^{101}-1\)
\(C=\frac{3^{101}-1}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Giải phương trình nghiệm nguyên
a) \(x^2+4x+2018^{10}\)
b) \(x^2+4x+\left(y-1\right)^2=21\)
c) \(x^2+3\left(y-1\right)^2=2021\)
d) \(\left(3x-1\right)^{2020}-18\left(y-2\right)^{2019}=2019^{2020}\)
2. Tìm x,y ∈ Z
a) \(x^2-y^2+6y=56\)
b) \(x^2-4x+9y^2-6y=11\)
\(1,\\ b,\Leftrightarrow\left(x^2+4x+4\right)+\left(y-1\right)^2=25\\ \Leftrightarrow\left(x+2\right)^2+\left(y-1\right)^2=25\)
Vậy pt vô nghiệm do 25 ko phải tổng 2 số chính phương
\(2,\\ a,\Leftrightarrow x^2-\left(y^2-6y+9\right)=47\\ \Leftrightarrow x^2-\left(y-3\right)^2=47\)
Mà 47 ko phải hiệu 2 số chính phương nên pt vô nghiệm
\(b,\Leftrightarrow\left(x-2\right)^2+\left(3y-1\right)^2=16\)
Mà 16 ko phải tổng 2 số chính phương nên pt vô nghiệm
Đúng 2
Bình luận (1)
1a. Đề lỗi
1b.
PT $\Leftrightarrow (x+2)^2+(y-1)^2=25$
$\Leftrightarrow (x+2)^2=25-(y-1)^2\leq 25$
$(x+2)^2$ là scp không vượt quá $25$ nên có thể nhận các giá trị $0,1,4,9,16,25$
Nếu $(x+2)^2=0\Rightarrow (y-1)^2=25$
$\Rightarrow (x,y)=(-2, 6), (-2, -4)$
Nếu $(x+2)^2=1\Rightarrow (y-1)^2=24$ không là scp (loại)
Nếu $(x+2)^2=4\Rightarrow (y-1)^2=21$ không là scp (loại)
Nếu $(x+2)^2=9\Rightarrow (y-1)^2=16$
$\Rightarrow (x,y)=(1, 5), (1, -3), (-5,5), (-5, -3)$
Nếu $(x+2)^2=25\Rightarrow (y-1)^2=0$
$\Rightarrow (x,y)=(3, 1), (-7, 1)$
Đúng 1
Bình luận (0)
1c.
Vì $x^2$ là scp nên $x^2\equiv 0,1\pmod 3$
$3(y-1)^2\equiv 0\pmod 3$
$\Rightarrow x^2+3(y-1)^2\equiv 0,1\pmod 3$
Mà $2021\equiv 2\pmod 3$
Do đó pt $x^2+3(y-1)^2=2021$ vô nghiệm
1d.
Ta thấy:
$(3x-1)^{2020}$ là scp không chia hết cho $3$ nên $(3x-1)^{2020}\equiv 1\pmod 3$
$18(y-2)^{2019}\equiv 0\pmod 3$
$\Rightarrow (3x-1)^{2020}+18(y-2)^{2019}\equiv 1\pmod 3$
Mà $2019^{2020}\equiv 0\pmod 3$
Do đó pt vô nghiệm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm x,y biết x^2018+y^2018=x^2019+y^2019=x^2020+y^2020.
Cho a+b+c=2019, 1/a + 1/b+1/c=1/2019. Tính 1/a^2019+1/b^2019+1/c^2019
Tìm x,y biết x^2-xy=6x-5y-8.
Giúp mk với, mk vã lắm rồi :-( :-(
gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> là sẽ tìm được nghiệm nguyên của
a) 2019/2020 x 4/11 + 2019/2020 x 5/11 + 2019/2020 x 2/11
b) 17/14 x 25/27 - 1/14 x 25/27 - 2/14 x 25/27
\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)
Đúng 0
Bình luận (0)
A=[ 2020 x 2019 + 2019 x 2018] x [ 1 + 1/2 : 1 và 1/2 - 1 và 1/3]
\(A=\left(2020\times2019+2019\times2018\right)\times\left(1+\dfrac{1}{2}:1\dfrac{1}{2}-1\dfrac{1}{3}\right)\)
\(A=\left[2019\times\left(2020+2018\right)\right]\times\left(1+\dfrac{1}{2}:\dfrac{3}{2}-\dfrac{4}{3}\right)\)
\(A=4038\times2019\times\left(1+\dfrac{1}{3}-\dfrac{4}{3}\right)\)
\(A=4038\times2019\times0\)
\(A=0\)
Đúng 1
Bình luận (0)
Tìm x,y,z:
a) |x+\(1\over101\)| + |x+\(2\over 101\)| +...+ |x+\(100\over 101\)|= 101x
b)(x-y)3 + (y-z)2 + |x-z|= 20192020
1/(x+1)(x+2) +1/(x+2)(x+3) +1/(x+3)(x+4)=2019/2020
\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{2019}{2020}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{2019}{2020}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{2019}{2020}\)
\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{2019}{2020}\)
\(\Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}=\dfrac{2019}{2020}\)
\(\Leftrightarrow\left(x+1\right)\left(x+4\right).2019=6060\)
<=> x = - 0,208387929
P/s: Số lạ zậy?Đề sai ko
Đúng 1
Bình luận (0)