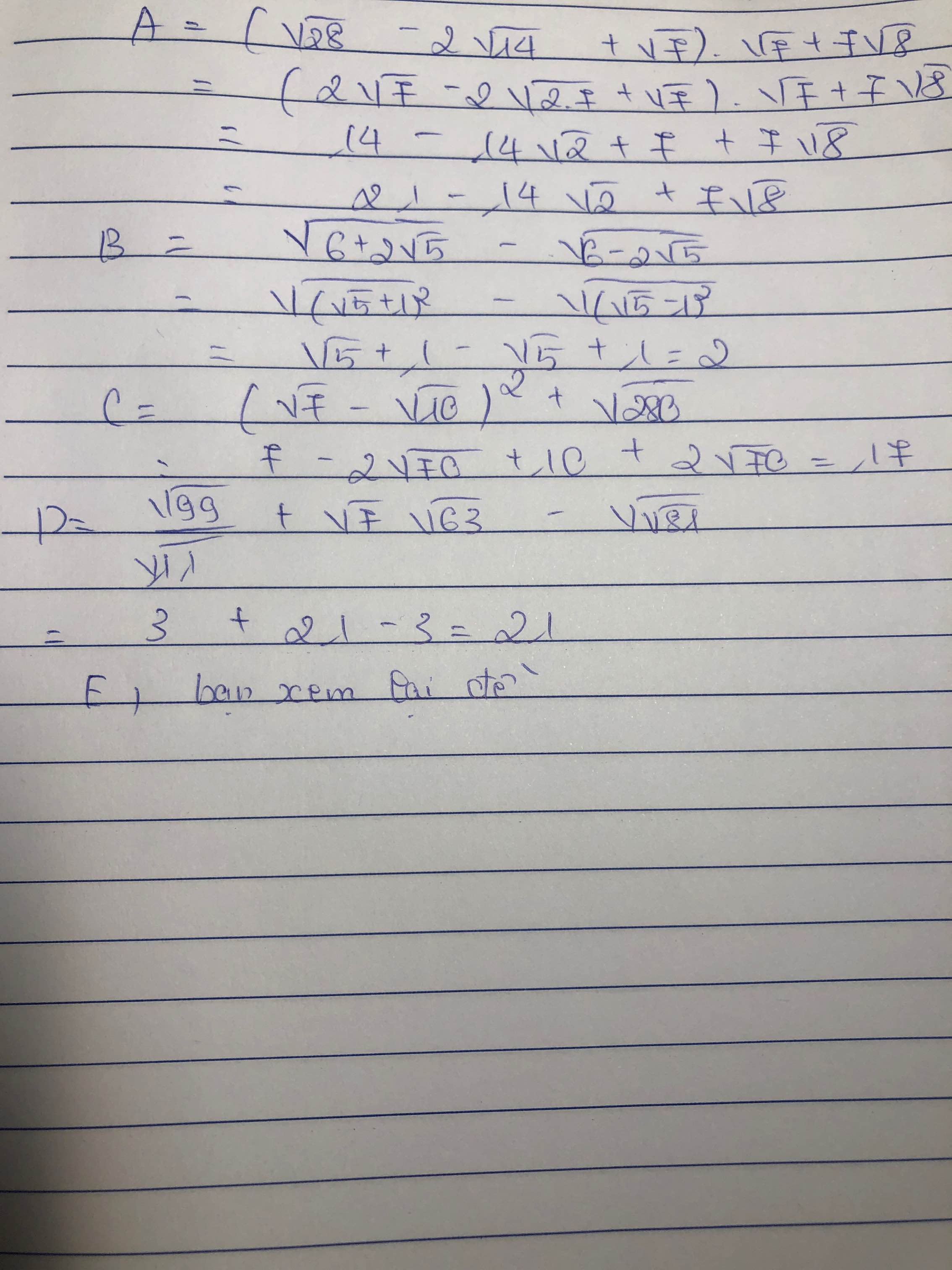\(=14-14\sqrt{2}+7+14\sqrt{2}=21\)

Bài 1:

a. Ta có \(\sqrt{\dfrac{2}{x^2}}=\dfrac{\sqrt{2}}{\left|x\right|}=\dfrac{\sqrt{2}}{x}\) ,để biểu thức có nghĩa thì \(x>0\)

b. Để biểu thức \(\sqrt{\dfrac{-3}{3x+5}}\) có nghĩa thì \(\dfrac{-3}{3x+5}\ge0\) 

mà \(-3< 0\Rightarrow3x+5< 0\) \(\Rightarrow x< \dfrac{-5}{3}\)

Bài 2:

a. \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(1-\sqrt{2}\right)}{1-2}=\dfrac{-\sqrt{2}}{-1}=\sqrt{2}\)

b. \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)

\(=14-14\sqrt{2}+7+14\sqrt{2}\)

\(=21\)

c. \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)

\(=14-6\sqrt{28}+18+6\sqrt{28}\)

\(=32\)

\(\sqrt{29-4\sqrt{7}}=\sqrt{\left(2\sqrt{7}\right)^2-2.2\sqrt{7}.1+1^2}=\sqrt{\left(2\sqrt{7}-1\right)^2}=\left|2\sqrt{7}-1\right|\)

\(=2\sqrt{7}-1\)

\(\sqrt{19+6\sqrt{2}}=\sqrt{\left(3\sqrt{2}\right)^2+2.3\sqrt{2}.1+1^2}=\sqrt{\left(3\sqrt{2}+1\right)^2}=\left|3\sqrt{2}+1\right|\)

\(=3\sqrt{2}+1\)

\(\sqrt{28-6\sqrt{3}}=\sqrt{\left(3\sqrt{3}\right)^2-2.3\sqrt{3}.1+1^2}=\sqrt{\left(3\sqrt{3}-1\right)^2}=\left|3\sqrt{3}-1\right|\)

\(=3\sqrt{3}-1\)

\(\sqrt{46-6\sqrt{5}}=\sqrt{\left(3\sqrt{5}\right)^2-2.3\sqrt{5}.1+1^2}=\sqrt{\left(3\sqrt{5}-1\right)^2}=\left|3\sqrt{5}-1\right|\)

\(=3\sqrt{5}-1\)

\(\sqrt{49+8\sqrt{3}}=\sqrt{\left(4\sqrt{3}\right)^2+2.4\sqrt{3}.1+1^2}=\sqrt{\left(4\sqrt{3}+1\right)^2}=\left|4\sqrt{3}+1\right|\)

\(=4\sqrt{3}+1\)

\(\sqrt{32-8\sqrt{7}}=\sqrt{\left(2\sqrt{7}\right)^2-2.2\sqrt{7}.2+2^2}=\sqrt{\left(2\sqrt{7}-2\right)^2}=\left|2\sqrt{7}-2\right|\)

\(=2\sqrt{7}-2\)

\(\sqrt{29-4\sqrt{7}}=2\sqrt{7}-1\)

\(\sqrt{19+6\sqrt{2}}=3\sqrt{2}+1\)

\(\sqrt{28-6\sqrt{3}}=3\sqrt{3}-1\)

\(\sqrt{46-6\sqrt{5}}=3\sqrt{5}-1\)

\(\sqrt{49+8\sqrt{3}}=4\sqrt{3}+1\)

\(\sqrt{32-8\sqrt{7}}=2\sqrt{7}-2\)

1) \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right).\sqrt{7}+7\sqrt{8}\)

Xin lỗi xin lỗi :v

1)\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right).\sqrt{7}+7\sqrt{8}\)

= \(\sqrt{7}.\left(3\sqrt{7}-2\sqrt{14}\right)+14\sqrt{2}\)

= 21 - \(14\sqrt{2}+14\sqrt{2}\)

= 21

2) \(\left(\sqrt{8}-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{18}-\sqrt{8}+\sqrt{5}\right)\)

= \(\left(2\sqrt{2}-\sqrt{2}-\sqrt{5}\right)\left(3\sqrt{2}+\sqrt{5}-2\sqrt{2}\right)\)

= \(\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)\)

=\(\left(\sqrt{2}\right)^2-\left(\sqrt{5}\right)^2\)

= -3

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\cdot\sqrt{7}+7\sqrt{8}\)

\(=\left(3\sqrt{7}-2\sqrt{14}\right)\cdot\sqrt{7}+14\sqrt{2}\)

\(=21-14\sqrt{2}+14\sqrt{2}\)

=21

Bạn ơi ! Cho mình hỏi,đề bài yêu cầu gì vậy bạn ?

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)

\(=\left(2\sqrt{7}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)

\(=14-14\sqrt{2}+7+7\sqrt{8}\)

\(=21-14\sqrt{2}+14\sqrt{2}=21\)

`a, (sqrt 28 - sqrt 12 - sqrt 7) sqrt 7 + 2 sqrt 21`.

`= sqrt(28.7) - sqrt(12.7) - sqrt(7.7) + 2 sqrt 21`.

`= sqrt(4. 7.7) - sqrt (12.7) - 7 + 2 sqrt 21`.

`= 14 - sqrt(4.3.7) - 7 + 2 sqrt 21`.

`= 7`.

`b, (sqrt99-sqrt18-sqrt11)sqrt11+3sqrt22`

`= sqrt(99.11)- sqrt(18.11)-sqrt(11.11) +3sqrt22`

`= sqrt(9.11.11)-sqrt(2.9.11)-11+3sqrt22`

`= 33 - 11 = 22`.

Lời giải:
\((\sqrt{28}-2\sqrt{14}+\sqrt{7})\sqrt{7}+7\sqrt{8}\)

\(=(2\sqrt{7}-2\sqrt{2}.\sqrt{7}+\sqrt{7})\sqrt{7}+14\sqrt{2}\)

\(=\sqrt{7}(2-2\sqrt{2}+1).\sqrt{7}+14\sqrt{2}\)

\(=7(3-2\sqrt{2})+14\sqrt{2}=21-14\sqrt{2}+14\sqrt{2}=21\)