chứng minh rằng ai = im

Những câu hỏi liên quan
Cho hình 43. Chứng minh rằng AI = IM.
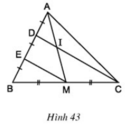
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
Đúng 0
Bình luận (0)
Chứng minh rằng AI = IM : Hình 43 SGK Toán 8
cho hình 43.Chứng minh rằng AI=IM
△BDC có ED = EB
MB = MC
⇒ EM là đường trung bình của tam giác này (Theo định nghĩa: đoạn thẳng nối trung điểm hai cạnh của một tam giác là đường trung bình của tam giác đó) ⇒ ME//CD
△AME có DA = DE (gt)
DI//ME (cmt)
⇒ IA = IM (Theo định lí: đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3)
Đúng 0
Bình luận (0)
\(\Delta BDC\) có BE=ED và BM=MC
nên EM// CD
\(\Rightarrow DI//EM\)
\(\Delta AEM\) có AD=DE và DI//EM
nên AI//IM
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ ( ).a) Chứng minh tam giác AKH là tam giác cânb) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .c) Chứng minh: .HK song song BC
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ ( ).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
c) Chứng minh: .HK song song BC
Bổ sung đề: Kẻ đường cao BH,CK(H∈AC; K∈AB)
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\hat{HAB}\) chung
Do đó: ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: Sửa đề: IM là phân giác của góc BIC
Xét ΔABC có
BH,CK là các đường cao
BH cắt CK tại I
Do đó: I là trực tâm của ΔABC
=>AI⊥BC tại M
Ta có: AK+KB=AB
AH+HC=AC
mà AK=AH và AB=AC
nên BK=HC
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
=>\(\hat{KCB}=\hat{HBC}\)
=>\(\hat{IBC}=\hat{ICB}\)
=>ΔIBC cân tại I
ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
c: Xét ΔABC có \(\frac{AK}{AB}=\frac{AH}{AC}\)
nên KH//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ ( ). a) Chứng minh tam giác AKH là tam giác cânb) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .c) Chứng minh: .HK song song BC
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ ( ).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
c) Chứng minh: .HK song song BC
Bổ sung đề: Kẻ đường cao BH,CK(H∈AC; K∈AB)
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\hat{HAB}\) chung
Do đó: ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: Sửa đề: IM là phân giác của góc BIC
Xét ΔABC có
BH,CK là các đường cao
BH cắt CK tại I
Do đó: I là trực tâm của ΔABC
=>AI⊥BC tại M
Ta có: AK+KB=AB
AH+HC=AC
mà AK=AH và AB=AC
nên BK=HC
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
=>\(\hat{KCB}=\hat{HBC}\)
=>\(\hat{IBC}=\hat{ICB}\)
=>ΔIBC cân tại I
ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
c: Xét ΔABC có \(\frac{AK}{AB}=\frac{AH}{AC}\)
nên KH//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, hai đường cao BH và CK ( ).
a) Chứng minh ∆ ABH∆ACK
b) Chứng minh tam giác AKH là tam giác cân
c) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
d) Chứng minh: .HK//BC
Đọc tiếp
Cho tam giác ABC cân tại A, hai đường cao BH và CK ( ).
a) Chứng minh ∆ ABH=∆ACK
b) Chứng minh tam giác AKH là tam giác cân
c) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
d) Chứng minh: .HK//BC
Cho ΔABC cân tại A, với đường trung tuyến AI: a, Chứng minh ΔABI = ΔACI b, Chứng minh AI vuông góc với BC c, Kẻ đường trung tuyến BM. Biết AC = 8 cm. Tính IM d, Chứng minh IM // AB Chỉ cần câu c và d
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
DO đó: ΔABI=ΔACI
b: Ta có:ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A, với đường trung tuyến AI: a, Chứng minh ΔABI = ΔACI b, Chứng minh AI vuông góc với BC c, Kẻ đường trung tuyến BM. Biết AC = 8 cm. Tính IM d, Chứng minh IM // AB Chỉ cần câu c và d
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: AC=8cm
nên AB=8(cm)
Xét ΔBAC có
I là trung điểm của BC
M là trung điểm của AC
Do đó: IM là đường trung bình
=>IM=AB/2=8/2=4(cm)
Đúng 0
Bình luận (0)
Cho hình 43. Chứng minh rằng AI = IM.
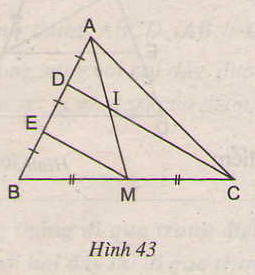
t/g DBC có :
ED = EB ( gt )
MB = MC ( gt )
Nên EM là đường trung bình của tam giác DBC
\(\Rightarrow\)EM // DC
T/g AEM có :
DA = DE ( gt )
DI // EM ( cmt , vì EM // DC )
Theo định lý 1 ta có :
AI = IM ( đpcm )
Đúng 0
Bình luận (0)
o0o Nguyễn Việt Hiếu o0o hướng chứng minh dùng đường trung bình của tam giác thì đúng
cơ mà định lí 1 là định lí nào? ghi như vậy không được
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

















