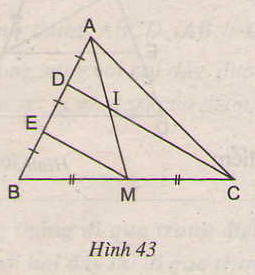
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
Chứng minh rằng AI = IM : Hình 43 SGK Toán 8
Cho hình 43. Chứng minh rằng AI = IM.
cho tam giác ABC, D thuộc AD sao cho: AD = 1/2 DC, AM là trung tuyến, I thuộc giao điểm của BD và AM. Chứng minh rằng AI=IM
cho tam giác ABC vuông tại A ( AB < AC ) , đường trung tuyến AI . Qua I vẽ IM vuông góc với AB ( M thuộc AB ) , IN vuông góc với AC ( N thuộc AC )
a) cho AB = 9cm ; AC = 12cm . Tính IM , IN,MN
b) chứng minh rằng tứ giác NMBI là hình bình hành
c) tam giác ABC vuông tại A có thêm điều kiện gì thì tứ giác BMNC là hình thang cân
cho tam giác ABC , điểm D thuộc cạnh AC sao cho AD = 1/2 ĐC . Gọi M là trung điểm của BC , Ịà giao điểm của BD và AM . Chứng minh rằng AI = IM
Cho tam giác ABC, điểm D thuộc cạch AC sao cho AD=1/2 DC. Gọi M là trung điểm của BC,I là giao điểm của BD và AM. Chứng minh rằng AI=IM.
: Cho ΔABC vuông tại A, đường trung tuyến AM . Gọi I là trung điểm của AC, Trên tia đối của tia IM lấy điểm K sao cho IK= IM . a) Chứng minh AMCK là hình thoi. b) Chứng minh AKMB là hình bình hành.
cho tam giác ABC vuông tại A ( AB < AC ) . Gọi I là trung điểm BC. Qua I vẽ IM vuông góc AB tại M và IN vuông góc AC tại N.
a): Chứng minh tứ giác AMIN là hình chữ nhật nhật
b)Chứng minh rằng tứ giác NMBI là hình bình hành
c)Cho IM=5cm .Tính độ dài NC
Làm gấp hộ mình câu B , C với , cần gấp lắm mình sẽ tick 3 acc cho bạn