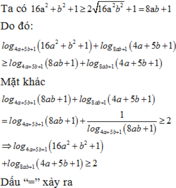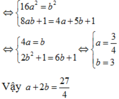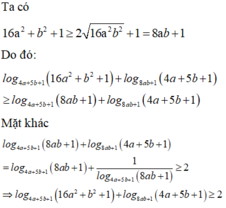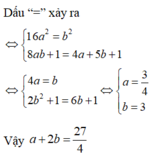cho a và b thỏa mãn 2b^2+5b^2-4ab+14b-8a+11=0

Những câu hỏi liên quan
1) Cho 3 số a,b,c thỏa mãn a+b+c=abc
CMR a(b^2-1)(c^2-1)+b(a^2-1)(c^2-1)+c(a^2-1)(b^2-1)=4abc
2) Cho a và b thỏa mãn 2a^2+5b^2-4ab+14b-8a+11=0
So sánh a=a^13+b^15 và B=a^15+b^13
1) ta có: a(b^2 -1)(c^2 -1)+b(a^2 -1)(c^2 -1)+c(a^2-1)(b^2-1)
=(ab^2 -a)(c^2-1)+(ba^2 -b)(c^2-1)+(ca^2-c)(b^2-1)
đén đây nhân bung ra hết rồi rút gọn và thay a+b+c=abc là đc
Đúng 0
Bình luận (0)
Cho hai số thực a,ba,b thỏa mãn \(a^2+4ab-5b^2=0\)(a≠b,a≠−b) Tính giá trị của biểu thức
Q=\(\dfrac{2a-b}{a-b}+\dfrac{3a-2b}{a+b}\)
`a^2+4ab-5b^2=0`
`<=>a^2+4ab+4b^2-9b^2=0`
`<=>(a+2b)^2-9b^2=0`
`<=>(a+2b-3b)(a+2b+3b)=0`
`<=>(a-b)(a+5b)=0`
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=-5b\end{matrix}\right.\)
`Q={2a-b}/{a-b}+{3a-2b}/{a+b}`
Với `a=b` `=>` giá trị vô nghĩa
Với `a=-5b`
`Q={-10b-b}/{-5b-b}+{-15b-2b}/{-5b+b}`
`Q={-11b}/{-6b}+{-17b}/{-4b}`
`Q=11/6+17/4`
`Q=73/12`
Đúng 3
Bình luận (0)
Cho
a
0
,
b
0
thỏa mãn
log
4
a
+
5
b
+
1
(
16
a
2
+
b
2
+
1
)
+
log
8
a
b...
Đọc tiếp
Cho a > 0 , b > 0 thỏa mãn log 4 a + 5 b + 1 ( 16 a 2 + b 2 + 1 ) + log 8 a b + 1 ( 4 a + 5 b + 1 ) = 2 . Giá trị của a + 2 b bằng
A. 27 4
B. 6
C. 9
D. 20 3
Cho a0; b0 thỏa mãn
log
4
a
+
5
b
+
1
16
a
2
+
b
2
+
1
+...
Đọc tiếp
Cho a>0; b>0 thỏa mãn log 4 a + 5 b + 1 16 a 2 + b 2 + 1 + log 8 a b + 1 4 a + 5 b + 1 = 2 Giá trị của a+2b bằng
A. 27 4
B. 6
C. 9
D. 20 3
Cho 2 số thực dương a,b thỏa mãn \(0< a,b\le1\)và \(a+b=4ab\).Tìm minP
\(P=a^2b+ab^2-\frac{a^2+b^2}{6a^2b^2}\)
P=a2b+ab2-\(\frac{\left(a+b\right)^2-2ab}{6a^2b^2}\)=a2b+ab2-\(\frac{\left(4ab\right)^2-2ab}{6a^2b^2}\)=a2b+ab2-\(\frac{16a^2b^2}{6a^2b^2}\)+\(\frac{2ab}{6a^2b^2}\)
=a2b+ab2-\(\frac{8}{3}\)+\(\frac{1}{3ab}\)
Áp dụng Bất đẳng thức Cauchy cho 3 số dương, ta được:
P==a2b+ab2-\(\frac{8}{3}\)+\(\frac{1}{3ab}\)\(\ge\)3.\(\sqrt[3]{a^3b^3\frac{8}{3}}\)+\(\frac{1}{3ab}\)=\(\frac{6}{\sqrt[3]{3}}\).ab+\(\frac{1}{3ab}\)
Áp dụng Bất đẳng thức Cauchy cho 2 số dương, ta được:
P=\(\frac{6}{\sqrt[3]{3}}\).ab+\(\frac{1}{3ab}\)\(\ge\)2.\(\sqrt{\frac{6}{\sqrt[3]{3}}.ab.\frac{1}{3ab}}\)=\(\frac{2\sqrt{6}}{\sqrt[6]{3}}\)
Vậy MinP=\(\frac{2\sqrt{6}}{\sqrt[6]{3}}\)
Đúng 0
Bình luận (0)
\(-\frac{8}{3}\)có phải là số không âm đâu mà áp dụng BĐT Cosi
Đúng 0
Bình luận (0)
P=a2b+ab2-\(\frac{\left(a+b\right)^2-2ab}{6a^2b^2}\)=a2b+ab2-\(\frac{8}{3}\)+\(\frac{1}{3ab}\)
Áp dụng Bất đẳng thức Cauchy cho 3 số dương, ta được:
P=a2b+ab2-\(\frac{8}{3}\)+\(\frac{1}{3ab}\)\(\ge\)3\(\sqrt[3]{a^3.b^3.1}\)-\(\frac{11}{3}\)+\(\frac{1}{3ab}\)=3ab-\(\frac{11}{3}\)+\(\frac{1}{3ab}\)
Áp dụng Bất đẳng thức Cauchy cho 2 số dương, ta được:
P=3ab-\(\frac{11}{3}\)+\(\frac{1}{3ab}\)=2\(\sqrt{3ab.\frac{1}{3ab}}\)-\(\frac{11}{3}\)=-\(\frac{5}{3}\)
Vậy MinP=-\(\frac{5}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a,b dương thỏa mãn hệ a^3-3a^2+5a-17=0 và b^3-3b^2+5b-11=0. Cmr: a+b=2
Xem chi tiết
Cho a,b thỏa mãn : a^3 - 3a^2 + 5a - 17=0 và b^3 - 3b^2 + 5b -11 = 0
tính a^2 +b^2
Cho số thực a, b thỏa mãn: a2+5b2-4ab+2b+1= 0
Hãy tính giá trị của biểu thức C = 5a3- y2019 .
\(a^2-4ab+5b^2+2b+1=0\)
\(\Leftrightarrow a^2-4ab+4b^2+b^2+2b+1=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(b+1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2b=0\\b+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\)
\(C=5a^3-b^{2019}=5\left(-2\right)^3-\left(-1\right)^{2019}=-40+1=-39\)
Đúng 0
Bình luận (0)
Cho a,b thỏa mãn : a^3 - 3a^2 + 5a - 17=0 và b^3 - 3b^2 + 5b -11 = 0
tính a^2 +b^2
giúp ! giúp vs :) please!