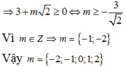Tìm giá trị m để hàm số y= \(\sqrt{sinx+m}\) có TXĐ D=R

Những câu hỏi liên quan
tìm tất cả giá trị của m để hàm số sau có tập xác định R
a)y=\(\sqrt{m-cosx}\)
b)y=\(\sqrt{2sinx-m}\)
c)y=\(\dfrac{sinx-1}{cosx+m}\)
a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để hàm số ym sinx+7x-5m+3 có y
≥
0,với mọi x thuộc R A. B. C. D.
Đọc tiếp
Tìm các giá trị của tham số m để hàm số y=m sinx+7x-5m+3 có y' ≥ 0,với mọi x thuộc R
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Đúng 2
Bình luận (3)
Tìm giá trị của m để hàm số y x + m(sinx + cosx + m ) luôn đồng biến trên R A.
-
2
2
≤
m
≤
2
2
B.
0
≤
m
≤
2
2
C.
-
2
2
≤
m
≤
0...
Đọc tiếp
Tìm giá trị của m để hàm số y = x + m(sinx + cosx + m ) luôn đồng biến trên R
A. - 2 2 ≤ m ≤ 2 2
B. 0 ≤ m ≤ 2 2
C. - 2 2 ≤ m ≤ 0
D. - 2 ≤ m ≤ 2
y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A
Đúng 0
Bình luận (0)
Tìm TXĐ của hàm số \(y=\dfrac{sinx}{\sqrt{3}sinx+cosx}\)
\(\sqrt{3}sinx+cosx\ne0\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx\ne0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)\ne0\)
\(\Leftrightarrow x+\dfrac{\pi}{6}\ne k\pi\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{6}+k\pi\)
Đúng 2
Bình luận (0)
Tìm m để TXĐ của hàm số \(y=\sqrt{\left(mx+3\right)\left(x-2\right)}\) là R
\(y\) có TXĐ là \(\mathbb{R}\) \(\Leftrightarrow (mx+3)(x-2) ≥0\)
TH1: \(\left[ \begin{array}{l}mx+3\\x-2=0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x=\dfrac{-3}{m} (m\ne0)\\x=2\end{array} \right.\)
TH2: \(\begin{cases}mx+3>0\\x-2>0\\\end{cases} \Leftrightarrow \begin{cases}x > \dfrac{-3}{m} \\x>2\\\end{cases} \)
TH3: \(\begin{cases}mx+3<0\\x-2<0\\\end{cases} \Leftrightarrow \begin{cases}x < \dfrac{-3}{m}\\x<2\\\end{cases} \)
Vậy...
Đúng 1
Bình luận (1)
Cho hàm số
y
sin
x
-
3
cos
x
-
m
x
. Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R A.
m
≤
-
2
B.
m
≤
-
3
C.
m
≥
2
D.
m
≥
1
Đọc tiếp
Cho hàm số y = sin x - 3 cos x - m x . Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R
A. m ≤ - 2
B. m ≤ - 3
C. m ≥ 2
D. m ≥ 1
Tìm tất cả các giá trị thực m để hàm số ysinx+cosx+mx đồng biến trên R. A.. B.. C.. D..
Đọc tiếp
Tìm tất cả các giá trị thực m để hàm số y=sinx+cosx+mx đồng biến trên R.
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn C
Ta có ![]()
![]() .
.
Vì ![]()
![]()
![]() .
.
![]()
![]() .
.
Để hàm số đã cho đồng biến trên ![]()
![]()
![]() ,
, ![]() .
.
![]()
![]()
![]()
![]() .
.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để hàm số y=3x+m(sinx + cosx +m) đồng biến trên R?
A. 5
B. 4
C. 3
D. Vô số