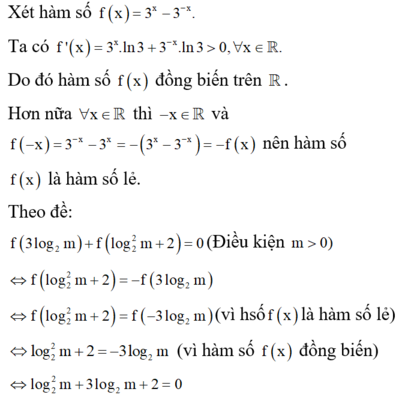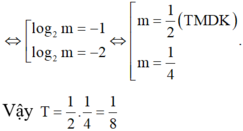1) Cho hàm số f(x)= 3x- 3-x. Gọi m1; m2 là các giá trị thực của tham số m để f(3log2m)+ f(log22m +2)= 0. Tính T=m1.m2
2) Cho hàm số y= -x3+ 2(m+1)x2- 3(m2-1)x+ 2 có đồ thị (Cm). Gọi M là điểm thuộc đồ thị có hoành độ xM= 1. Có bao nhiêu giá trị thực của tham số m sao cho tiếp tuyến của (Cm) tại điểm M song song với đường thẳng y= -3x+ 4.
3) Số giá trị nguyên của tham số m để phương trình sinx+ (m-1)cosx= 2m- 1 có nghiệm là ?
4) Giả sử z là các số phức thỏa mãn \(\left|1z-2-i\right|\)= 3. Giá trị lớn nhất của biểu thức 2\(\left|z-4-i\right|\)+\(\left|z+5+8i\right|\) bằng
5) Trong không gian Oxyz, cho mặt cầu (S): x2+ y2+ z2= 9 và mặt phẳng (P): 4x+ 2y+ 4z+7= 0. hai mặt cầu có bán kính R1 và R2 chứa đường giao tuyến của (S) và (P) đồng thời cùng tiếp xúc với mặt phẳng (Q): 3y- 4z- 20= 0. Tổng R1+ R2= ?