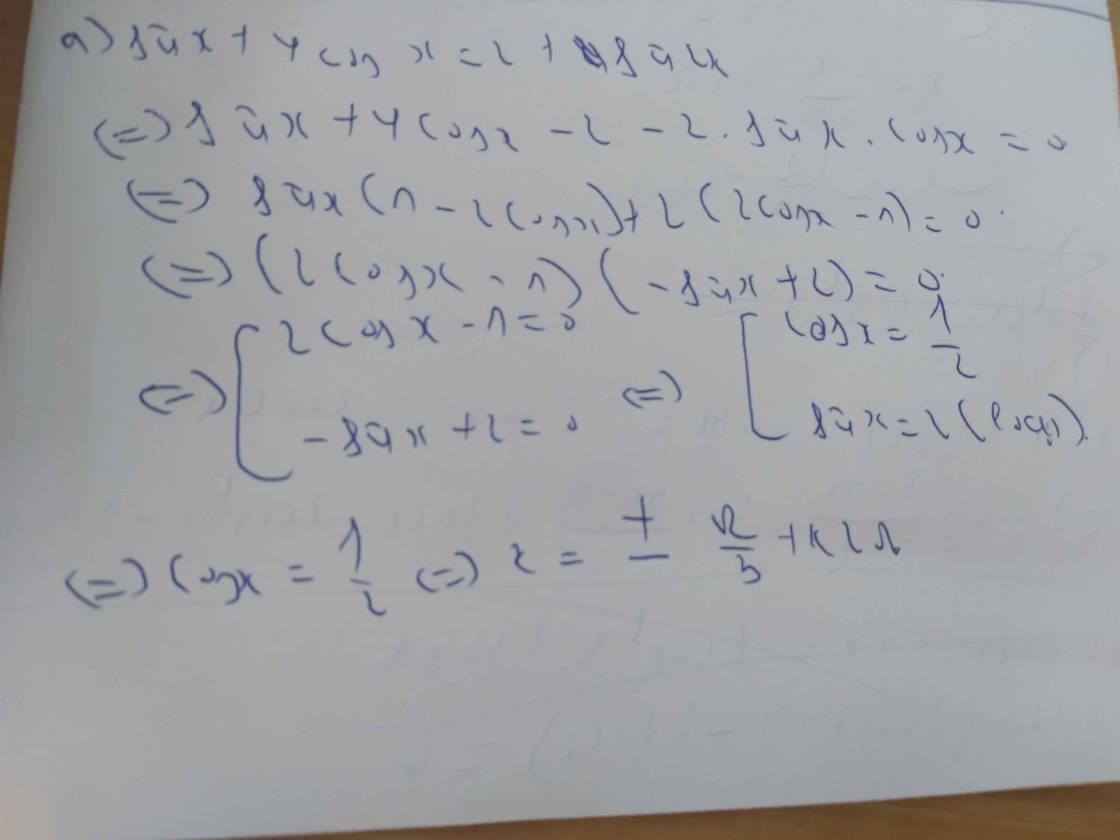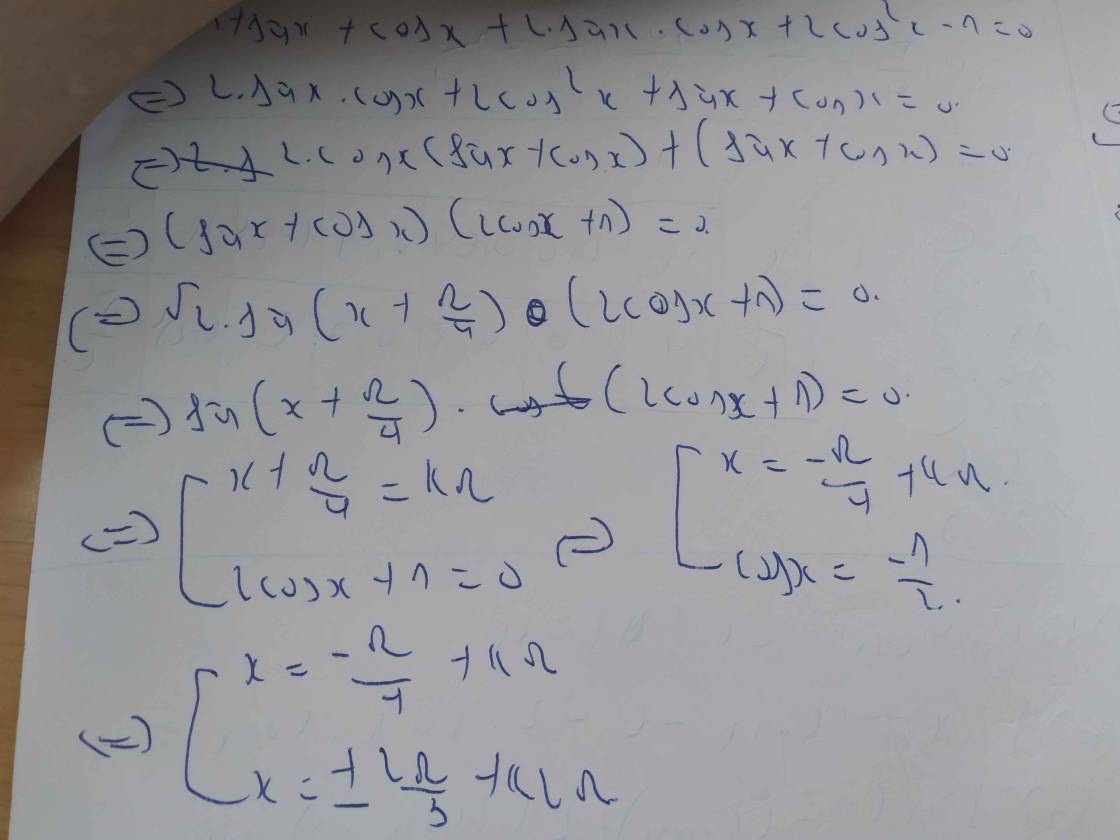Chứng minh rằng: (cos2x-sin2x)2+2(sin3x-sinx).cos-sin2x=cos2x, \(\forall x\in R\)

Những câu hỏi liên quan
Chứng minh rằng:
\(\left(cos2x-sin2x\right)^2+2\left(sin3x-sinx\right)cosx-1=0\), \(\forall x\in R\)
\(\left(cos2x-sin2x\right)^2+2\left(sin3x-sinx\right).cosx-1\)
\(=2sin^2\left(2x-\frac{\pi}{4}\right)+4cos2x.sinx.cosx-1\)
\(=1-cos\left(4x-\frac{\pi}{2}\right)+2sin2x.cos2x-1\)
\(=-cos\left(\frac{\pi}{2}-4x\right)+sin4x\)
\(=-sin4x+sin4x=0\)
Đúng 0
Bình luận (0)
\(sinx+4cosx=2+sin2x\)
\(\left(1-sin2x\right)\left(sinx+cosx\right)=cos2x\)
\(1+sinx+cosx+sin2x+cos2x=0\)
\(sinx+sin2x+sin3x=1+cosx+cos2x\)
\(sin^22x-cos^28x=sin\left(\dfrac{17\pi}{2}+10x\right)\)
Giúp mình với mn...
1)cos2x+cos22x+cos23x+cos24x=2
2) (1-tanx) (1+sin2x)=1+tanx
3) tan2x=sin3x.cosx
4) tanx +cot2x=2cot4x
5) sinx+sin2x+sin3x=cosx+cos2x+cos3x
6)sinx=√2 sin5x-cosx
7) 1/sin2x + 1/cos2x =2/sin4x
8) sinx+cosx=cos2x/1-sin2x
9)1+cos2x/cosx= sin2x/1-cos2x
10)sin3x+cos3x/2cosx-sinx=cos2x
sinx + sin2x + sin3x = 1 + cosx + cos2x
cos3x + sin3x + cosx - sinx = \(\sqrt{2}\)cos2x
sinx + sin2x + sin3x = cosx + cos2x + cos3x
b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)
c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)
\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức :
a) sin3x = 3sinx - 4sin3x
b) tan 2x + 1/cos2x = 1-2sin2x/1-sin2x
c) (cosx+sinx/cosx-sinx) - (cosx-sinx/cosx+sinx) = 2tan 2x
d) sin2x/1+cos2x = tanx
e)
a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)
\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)
\(=3sinx-4sin^3x\)
b/
\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)
\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)
\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)
c/
\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)
\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)
d/
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)
e/
Đúng 0
Bình luận (0)
1) sin3x+sin2x+sinx=cos2x+cosx+1
2) cos2x + cos23x = sin22x
\(1.sin3x+sin2x+sinx=cos2x+cosx+1\)
\(\Leftrightarrow2sin2x.cosx+sin2x=2cos^2x+cosx\)
\(\Leftrightarrow sin2x\left(2cosx+1\right)-cosx\left(2cosx+1\right)=0\\\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sin2x-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\sin2x=sin\left(\frac{\Pi}{2}-x\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm\frac{\Pi}{3}+k2\Pi\\x=\frac{\Pi}{6}+m2\Pi orx=\frac{\Pi}{2}+k2\Pi\end{matrix}\right.\)
\(2.cos^2x+cos^23x=sin^22x\)
\(\Leftrightarrow2+cos2x+cos6x=1-cos4x\)
\(\Leftrightarrow1+cos2x+cos6x+cos4x=0\)
\(\Leftrightarrow2cos^2x+2cos5x.cosx=0\)
\(\Leftrightarrow2cosx\left(cosx+cos5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\Pi}{2}+k\Pi\\cos5x=cos\left(\Pi-x\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\Pi}{2}+k\Pi\\5x=\Pi-x+k2\Pi or5x=x-\Pi+k2\Pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
(Sinx -sin3x)/√2 sinx = sin2x +cos2x
a)căn 3 sin4x-cos4x-2cosx=0
b)cosx +căn 3 cos2x-căn 3 sinx-sin2x=0
c)cos 3x+sin2x=căn 3(sin3x+cos2x)
d)cosx +căn 3=3-3/cosx+căn 3 sinx+1
a/
\(\sqrt{3}sin4x-cos4x=2cosx\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin4x-\frac{1}{2}cos4x=cosx\)
\(\Leftrightarrow sin\left(4x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\frac{\pi}{6}=\frac{\pi}{2}-x+k2\pi\\4x-\frac{\pi}{6}=\frac{\pi}{2}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2\pi}{15}+\frac{k2\pi}{5}\\x=\frac{2\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/
\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x-\sqrt{3}cos2x\)
\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=sin\left(2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(\frac{\pi}{6}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}-x+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow cos3x-\sqrt{3}sin3x=\sqrt{3}cos2x-sin2x\)
\(\Leftrightarrow\frac{1}{2}cos3x-\frac{\sqrt{3}}{2}sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(3x+\frac{\pi}{3}\right)=cos\left(2x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\3x+\frac{\pi}{3}=-2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=-\frac{\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) chứng minh không phụ thuộc vào x
Q= [(1-sinx-cos2x+sin3x)/(cosx+sin2x+cos3x)]*tan(x-(pi/2)
b) chứng minh:
cos 5x*cos 3x+sin 7x*sin x=2cos^3 2x -2 cos^2 x +1