\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x-4\right)}{\left(x-2\right)\left(x+2\right)}\le0\)

Bảng xét dấu:

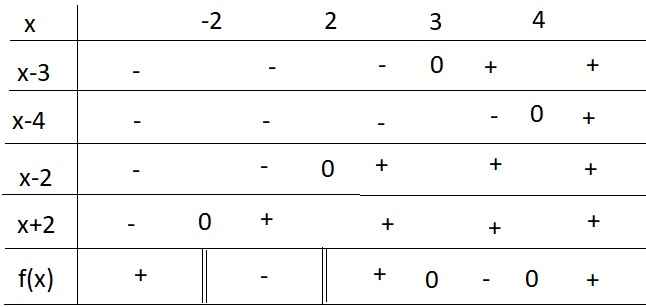
Từ bảng xét dấu ta được nghiệm của BPT là: 

\(\left[{}\begin{matrix}-2< x< 2\\3\le x\le4\end{matrix}\right.\)

\(\Leftrightarrow\) \(\begin{cases}x\le1;2\le x\\-3\le x\le4\\x\le-2;2\le x\end{cases}\)  \(\Leftrightarrow\)  \(\begin{cases}-3\le x\le-2\\2\le x\le4\end{cases}\)

Vậy hệ đã cho có tập nghiệm T = \(\left[-3;-2\right]\cup\left[2;4\right]\)

\(\frac{x^2\left(x+2\right)}{\left(x-1\right)\left(2x-1\right)}\le0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x\le-2\\\frac{1}{2}< x< 1\end{matrix}\right.\)

\(\begin{cases}x^2+7x-8\le0\\a^2x+1>3+\left(3a-2\right)x\end{cases}\) (1)

\(\Leftrightarrow\) \(\begin{cases}x^2+7x-8\le0\\\left(a^2-3a+2\right)x>2\end{cases}\)

ta đặt 

\(x^2+7x-8\le0\)  (a)

\(\left(a^2-3a+2\right)x>2\) (b)

(1) Vô nghiệm khi và chỉ khi T(a)\(\cap\)T(b) = \(\varnothing\)

Dễ thấy T(a) = \(\left[-8;1\right]\). Đặt m:=\(a^2-3a+2\), xét các trường hợp sau : 

- Nếu a=1 hoặc a=2 thì 

\(\left(a^2-3a+2\right)x>2\) \(\Leftrightarrow\) 0.x > 2 \(\Rightarrow\) T ( b) = \(\varnothing\) nên (1) vô nghiệm

- Nếu \(a\in\left(-\infty;1\right)\cup\left(2;+\infty\right):=\)(*) thì m >0 nên T(b) có nghiệm \(x>\frac{2}{m}\) Ta có :

T(a)\(\cap\) T(b) = \(\varnothing\)   \(\Leftrightarrow\)  \(\frac{2}{m}\ge1\)

                             \(\Leftrightarrow\)  \(2\ge m=a^2-3a+2\) ( do m>0 trong (*)

                            \(\Leftrightarrow\) \(a^2-3a\le0\)  \(\Leftrightarrow\)  \(0\le a\le3\)

Kết hợp với điều kiện \(a\in\)(*) được \(0\le a<1\) hoặc 2<a\(\le\)3

- Nếu \(a\in\)(1;2) thì m<0 nên T(b) có nghiệm \(x<\frac{2}{m}\) Ta có T(a)\(\cap\) T(b) = \(\varnothing\)   \(\Leftrightarrow\)  \(\frac{2}{m}\le-8\)

\(\Leftrightarrow\) \(2\ge-8m=-8\left(a^2-3a+2\right)\) (do m<0 trong (1;2) 

\(\Leftrightarrow\) \(4a^2-12a+9\ge0\)  \(\Leftrightarrow\) \(\left(2a-3\right)^2\ge0\) luôn đúng

Vậy với  \(a\in\)(1;2) thì (1) vô nghiệm. Tóm lại ta được 0\(\le a\le\)3 là các giá trị cần tìm

Đkxđ: \(x\ne2;x\ne3\)

Ta có \(x^2-3x+9=\left(x-\frac{3}{2}\right)^2+\frac{27}{4}\ge\frac{27}{4}>0\)

\(\Rightarrow\frac{x^2-3x+9}{x^2-5x+6}< 0\)khi và chỉ khi \(x^2-5x+6< 0\Leftrightarrow\left(x-2\right)\left(x-3\right)< 0\)

Vì \(x-2>x-3\Rightarrow\hept{\begin{cases}x-2>0\\x-3< 0\end{cases}\Rightarrow2< x< 3}\)

Vậy \(2< x< 3\)

\(a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\)

\(=>bpt:x^2+2x+2\le0\left(vo-li\right)\)

=>bpt vô nghiệm

\(b,4x^2-4x+5=\left(2x-1\right)^2+4\ge4>0\)

\(=>bpt:4x^2-4x+5\le0\left(vo-li\right)\)

=>bpt vô  nghiệm

a, \(< =>x^2+2x+1+1\le0\)

\(< =>\left(x+1\right)^2+1\le0\) vô nghiệm với mọi x thuộc R

b, \(< =>\left(2x-1\right)^2+4\le0\)vô nghiệm với mọi x thuộc R

\(a.\)

\(x^2+2x+2=x^2+2x+1+1\)

\(=\left(x+1\right)^2+1\ge1\)

\(b.\)

\(4x^2-4x+5=4x^2-4x+1+4\)

\(=\left(2x-1\right)^2+4\ge4\)

Bất phương trình bậc nhất 2 ẩn :

 \(2x+3y>0\Rightarrow Câu\) \(C\)

 \(x-2y\le1\Rightarrow Câu\) \(f\)

\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)

\(\Leftrightarrow4x-4+5y-15-2x+9>0\)

\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)