Tìm x, y >0 sao cho
( x2+y+3/4) (y2 + x +3/4) = ( 2x +1/2) (2y + 1/2 )
Những câu hỏi liên quan
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 - 2 h o ặ c 10 + 2
C. 10 - 2 2 h o ặ c 10 + 2 2
D. 10 - 2
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
l
o
g
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
Tìm m để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
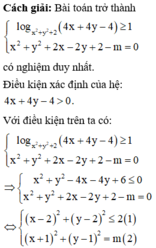
Trong tất cả các cặp (x;y) thỏa mãn l o g x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
Trong tất cả các cặp (x; y) thỏa mãn
log
x
2
+
y
2
+
2
(
4
x
+
4
y
-
4
)
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho
x
2
+
y...
Đọc tiếp
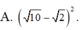
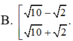
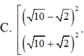
Trong tất cả các cặp (x; y) thỏa mãn log x 2 + y 2 + 2 ( 4 x + 4 y - 4 ) ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. ( 10 - 2 ) 2
B. 10 + 2
C. ( 10 + 2 ) 2
D. 10 - 2
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m n...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
Bài 1: Rút gọn các biểu thức:a. (2x - 1)2 - 2(2x - 3)2 + 4 b. (3x + 2)2 + 2(2 + 3x)(1 - 2y) + (2y - 1)2 c. (x2 + 2xy)2 + 2(x2 + 2xy)y2 + y4 d. (x - 1)3 + 3x(x - 1)2 + 3x2(x -1) + x3 e. (2x + 3y)(4x2 - 6xy + 9y2) f. (x - y)(x2 + xy + y2) - (x + y)(x2 - xy + y2) g. (x2 - 2y)(x4 + 2x2y + 4y2) - x3(x – y)(x2 + xy + y2) + 8y3
Đọc tiếp
Bài 1: Rút gọn các biểu thức:
a. (2x - 1)2 - 2(2x - 3)2 + 4
b. (3x + 2)2 + 2(2 + 3x)(1 - 2y) + (2y - 1)2
c. (x2 + 2xy)2 + 2(x2 + 2xy)y2 + y4
d. (x - 1)3 + 3x(x - 1)2 + 3x2(x -1) + x3
e. (2x + 3y)(4x2 - 6xy + 9y2)
f. (x - y)(x2 + xy + y2) - (x + y)(x2 - xy + y2)
g. (x2 - 2y)(x4 + 2x2y + 4y2) - x3(x – y)(x2 + xy + y2) + 8y3
a: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1+4-2\left(4x^2-12x+9\right)\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
e: \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)=8x^3+27y^3\)
Đúng 2
Bình luận (0)
a) (2x+1)2+(2x+3)2-2(2x+1)(2x+3)
b) (2x-3)(2x+3)-(x-+5)2-(x-1)(x+2)
c) (24x2y3z2-12x3y2z3+36x2y2z2):(-6x2y2z2)
d) (x+2y)(x2-2xy+4y2)-(x-y)(x2+xy+y2)
e) (x3+4x2-x-4):(x+4)
f) x2(x+y)+y2(x+y)+2x2y+2xy2
g) (x+y)2+(x-y)2-2(x+y)(x-y)
h) (a+b)2-(a-b)3-2b3
i) (x-y)(x+y)(x2+y2)(x4+y4)
Mong mọi người giúp đỡ vì mai em phải nộp
a) (2x + 3y)2 b) (x + dfrac{1}{4})2c) (x2 + dfrac{2}{5}y) . (x2 - dfrac{2}{5}y)d) (2x + y2)3e) (3x2 - 2y)2f) (x + 4) (x2 - 4x + 16)g) (x2 - dfrac{1}{3}) . (x4 + dfrac{1}{3}x2 + dfrac{1}{9})
Đọc tiếp
a) (2x + 3y)2
b) (x + \(\dfrac{1}{4}\))2
c) (x2 + \(\dfrac{2}{5}\)y) . (x2 - \(\dfrac{2}{5}\)y)
d) (2x + y2)3
e) (3x2 - 2y)2
f) (x + 4) (x2 - 4x + 16)
g) (x2 - \(\dfrac{1}{3}\)) . (x4 + \(\dfrac{1}{3}\)x2 + \(\dfrac{1}{9}\))
a) \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=4x^2+12xy+9y^2\)
b) \(\left(x+\dfrac{1}{4}\right)^2=x^2+2\cdot x\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
c) \(\left(x^2+\dfrac{2}{5}y\right)\left(x^2-\dfrac{2}{5}y\right)=\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
d) \(\left(2x+y^2\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3=8x^3+12x^2y^2+6xy^4+y^6\)
e) \(\left(3x^2-2y\right)^2=\left(3x^2\right)^2-2\cdot3x^2\cdot2y+\left(2y\right)^2=9x^4-12x^2y+4y^2\)
f) \(\left(x+4\right)\left(x^2-4x+16\right)=x^3+4^3=x^3+64\)
g) \(\left(x^2-\dfrac{1}{3}\right)\cdot\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)=\left(x^2\right)^3-\left(\dfrac{1}{3}\right)^3=x^6-\dfrac{1}{27}\)
Đúng 1
Bình luận (0)
c) C x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D x3(y−z)+y3(z−x)+z3(x−y).
e) E (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 0.
d) 3x(x+4)−x2 −4x 0.
f) (x−1)(x−3)(x+5)(x+7)−297 0.
(2x−1)2 −(x+3)2 0.
c) x3 −x2 +x+3 0.
e) (x2 +x+1)(x2 +x)−2 0.
a) A x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đọc tiếp
c) C = x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D = x3(y−z)+y3(z−x)+z3(x−y).
e) E = (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 = 0.
d) 3x(x+4)−x2 −4x = 0.
f) (x−1)(x−3)(x+5)(x+7)−297 = 0.
(2x−1)2 −(x+3)2 = 0.
c) x3 −x2 +x+3 = 0.
e) (x2 +x+1)(x2 +x)−2 = 0.
a) A = x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B = x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C = x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đề bài yêu cầu gì vậy em.
Đúng 0
Bình luận (0)
Bài 1: Rút gọn các biểu thức:a. (2x - 1)2 - 2 (2x - 3)2 + 4 b. (3x + 2)2 + 2 (2 + 3x) (1 - 2y) + (2y - 1)2 c. (x2 + 2xy)2 + 2 (x2 + 2xy) y2 + y4 d. (x - 1)3 + 3x (x - 1)2 + 3x2 (x -1) + x3 e. (2x + 3y) (4x2 - 6xy + 9y2) f. (x - y) (x2 + xy + y2) - (x + y) (x2 - xy + y2) g. (x2 - 2y) (x4 + 2x2y + 4y2) - x3 (x – y) (x2 + xy + y2) + 8y3
Đọc tiếp
Bài 1: Rút gọn các biểu thức:
a. (2x - 1)2 - 2 (2x - 3)2 + 4
b. (3x + 2)2 + 2 (2 + 3x) (1 - 2y) + (2y - 1)2
c. (x2 + 2xy)2 + 2 (x2 + 2xy) y2 + y4
d. (x - 1)3 + 3x (x - 1)2 + 3x2 (x -1) + x3
e. (2x + 3y) (4x2 - 6xy + 9y2)
f. (x - y) (x2 + xy + y2) - (x + y) (x2 - xy + y2)
g. (x2 - 2y) (x4 + 2x2y + 4y2) - x3 (x – y) (x2 + xy + y2) + 8y3
a: Ta có: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1-2\left(4x^2-12x+9\right)+4\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
b: \(\left(3x+2\right)^2+2\left(3x+2\right)\left(1-2y\right)+\left(1-2y\right)^2\)
\(=\left(3x+2+1-2y\right)^2\)
\(=\left(3x-2y+3\right)^2\)
Đúng 0
Bình luận (0)