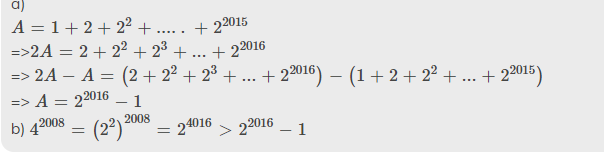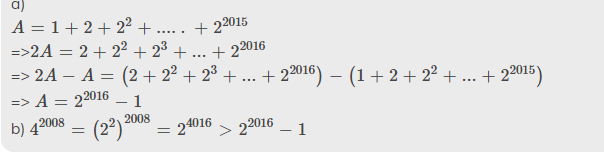so sánh a và b nếu: a^2 + b^2/2 = (a+b/2)^2

Những câu hỏi liên quan
So sánh số a và số b nếu: x > 2 ⇔ (a – b)x < 2(a – b)
Ta có: x > 2 ⇔ (a – b)x < 2(a – b)
⇒ a – b < 0 ⇔ a < b
Đúng 0
Bình luận (0)
Câu 1: Cho số thực m. Chứng minh:
a) m-4<m-3
b) -2-m>-3-m
c) Nếu m-3>5 thì m+2>8
d) m2+2>=2
Câu 2: Cho 2 số a, b
a) So sánh a, b. Biết a-3>b-3
b) So sánh 2a và a+b. Biết a+1>b+1
Câu 3: Cho a>b và x>y. Chứng minh a+x=b+y
Câu 4: Cho a, b, c>0. Chứng minh: a/b+b/c>=2
so sánh a^2+b^2 và ( a-b) ^ 2
A=(a-b)^2-a^2-b^2
=-2ab
(a-b)^2>=a^2+b^2
=>A>=0
=>ab<=0
(a-b)^2<a^2+b^2
=>A<0
=>ab>0
Đúng 2
Bình luận (1)
Ta có:
\(\left(a-b\right)^2=\left(a-b\right)\left(a-b\right)=a^2-ab-ab+b^2=a^2-2ab+b^2=a^2+b^2-2ab\)
\(\Rightarrow a^2+b^2>a^2+b^2-2ab\) hay \(a^2+b^2>\left(a-b\right)^2\) (nếu 2 số a và b là số dương)
\(\Rightarrow a^2+b^2< a^2+b-2ab\) hay \(a^2+b^2< \left(a-b\right)^2\) ( nếu trong 2 số a hoặc b có một số là số âm)
Đúng 2
Bình luận (0)
A = 1 + 2 + $2^{2}$ + .... + $2^{2015}$ và B = $4^{2008}$
a) Rút gọn tổng A
b) So sánh A và B
A = 1 + 2 + $2^{2}$ + .... + $2^{2015}$ và B = $4^{2008}$
a) Rút gọn tổng A
b) So sánh A và B
a)
`A = 1 + 2 + 2^2 + .....+2^2015`
=>`2A = 2 + 2^2 + 2^3 + ... + 2^2016`
=> `2A - A= (2 + 2^2 + 2^3 + ... + 2^2016)-(1 + 2 + 2^2 + ... + 2^2015)`
=> `A = 2^2016 - 1`
b) `4^2008 = (2^2)^2008 = 2^4016 > 2^2016 - 1`
Đúng 4
Bình luận (0)
A = 1 + 2 + $2^{2}$ + .... + $2^{2015}$ và B = $4^{2008}$
a) Rút gọn tổng A
b) So sánh A và B
so sánh:
:a^2 +b^2 và (a + b)^2 ,với a thuộc N* và b thuộc N*
\(\left(a+b\right)^2=a^2+b^2+2ab\)
Mà \(a,b\in\) N*
⇒2ab>0
⇒\(a^2+b^2+2ab>a^2+b^2\)
Đúng 1
Bình luận (0)
So sánh
A=a*b/a^2+b^2 và B=a^2+b^2/(a+b)^2
với a;b thuộc N* và a khác b
A = ab/a^2+b^2 < = ab/2ab = 1/2
B = a^2+b^2/(a+b)^2 = a^2+b^2/a^2+2ab+b^2 >= a^2+b^2/a^2+a^2+b^2+b^2 = 1/2
=> A < = B
Tk mk nha
Đúng 0
Bình luận (0)
Cho A = \(1+2+2^2+...+2^{2021}\) và B = \(2^{2022}\). So sánh A và B.
`# \text {DNamNgV}`
\(A=1+2+2^2+...+2^{2021}\text{ và }B=2^{2022}\)
Ta có:
\(A=1+2+2^2+...+2^{2021}\\ \Rightarrow2A=2+2^2+2^3+...+2^{2022}\\\Rightarrow2A-A=\left(2+2^2+2^3+...+2^{2022}\right)-\left(1+2+2^2+...+2^{2021}\right)\\ \Rightarrow A=2+2^2+2^3+...+2^{2022}-1-2-2^2-...-2^{2021}\\ \Rightarrow A=2^{2022}-1\)
Vì \(2^{2022}-1< 2^{2022}\)
\(\Rightarrow A< B.\)
Đúng 2
Bình luận (0)
cho 2 số hữu tỉ a/b và c/d (b>0 d>0).chứng minh rằng :nếu a/b<c/d thì a/b<a+c/b+d
áp dụng so sánh -2/3 và 3/5