Với a>0, b>0, b#1/4, rút gọn bt: \(\frac{a+\sqrt{a}+\frac{1}{4}}{2\sqrt{a}+1}\) : \(\frac{4b-1}{8\sqrt{b}-4}\)

Những câu hỏi liên quan
B1 . Đưa thừa số ra ngoài dấu căn : a. √5a² ( với a ≤ 0) b. √9b³ ( với b ≤ 0 ) c. √72a²b⁴ ( với a < 0 ) d . √24a⁴b⁸ ( a , b € R ) Giúp mình với ạ
a: \(\sqrt{5a^2}=\left|a\sqrt{5}\right|=-a\sqrt{5}\left(a< =0\right)\)
c: A=\(\sqrt{72a^2b^4}=\sqrt{36a^2b^4\cdot2}=6\sqrt{2}\cdot b^2\cdot\left|a\right|\)
mà a<0
nên \(A=-6\sqrt{2}\cdot ab^2\)
d: \(\sqrt{24a^4b^8}=\sqrt{4a^4b^8\cdot6}=2a^2b^4\cdot\sqrt{6}\)
Đúng 1
Bình luận (0)
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
-Giúp mình giải toán với!
+PHÂN TÍCH CÁC ĐA THỨC SAU THÀNH NHÂN TỬ.
A) 4+2c với c<0
B) a+b+2 căn ab với a>hoặc =0, b> hoặc =0
C) a+b-2 căn ab với a> hoặc =0, b>hoặc=0
b, \(a+b+2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}+2\sqrt{ab}=\left(\sqrt{a}+\sqrt{b}\right)^2\) ( Vì a, b >= 0 )
c, \(a+b-2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}-2\sqrt{ab}=\left(\sqrt{a}-\sqrt{b}\right)^2\)( Vì a, b >= 0 )
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(0;a) : B( b;0) và C(-b;0) với a; b 0.Viết phương trình đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C.
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(0;a) : B( b;0) và C(-b;0) với a; b > 0.Viết phương trình đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C.
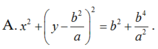
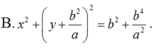
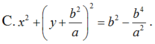
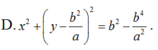
Đáp án B
Do đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C
Nên tam giác ABC cân tại A
tâm I của (C) thuộc Oy nên I(0; y0)
![]()
Do:
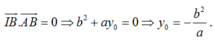
Mặc khác:
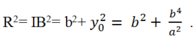
Vậy phương trình của là:
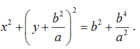
Đúng 0
Bình luận (0)
trong măt phang Oxy cho 3 điểm A(0;a), B(b;0) Và C(-b;0) với a>0 b>0. Tìm toa độ tâm I của đưong tròn tiếp xúc với AB tai B Và tiếp xúc với AC tại C
\(AB=AC=\sqrt{a^2+b^2}\) (1)
Do (C) tiếp xúc AB tại B và AC tại C \(\Rightarrow IA=IB=R\) (2)
Từ (1) và (2) \(\Rightarrow IA\) là trung trực của BC
Mà B và C nằm trên Ox, A nằm trên Oy \(\Rightarrow I\) nằm trên Oy \(\Rightarrow I\left(0;y\right)\)
\(\Rightarrow IA=y_A-y_I=a-y\)
Theo hệ thức lượng ta có:
\(IA.OA=AB^2\Leftrightarrow IA=\frac{AB^2}{OA}\Leftrightarrow a-y=\frac{a^2+b^2}{a}\)
\(\Rightarrow y=a-\frac{a^2+b^2}{a}=\frac{-b^2}{a}\Rightarrow I\left(0;-\frac{b^2}{a}\right)\)
Đúng 0
Bình luận (0)
Cho m = a.b.c^2 với a,b,a,b,c € z .biết m<0 ,a>0 ,c<0 . hãy so sánh b với số 0
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P). A. 2017 B.
2014
3
C.
2016
3
D.
2015...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).
A. 2017
B. 2014 3
C. 2016 3
D. 2015 3
Hệ thức nào sau đây phù hợp với quá trình nén khí đẳng nhiệt ?
A. Q + A = 0 với A < 0
B. ∆ U = Q + A với ∆ U > 0 ; Q < 0 ; A > 0.
C. Q + A = 0 với A > 0.
D. ∆ U = A + Q với A > 0 ; Q < 0.
\(\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}-\dfrac{a-b}{\sqrt{a}-\sqrt{b}}\) với \(a>0,b>0;a\ne b\)
giúp mk với!!!
`(asqrtb-bsqrta)/sqrt{ab}-(a-b)/(sqrta-sqrtb)`
`=(sqrt{ab}(\sqrta-sqrtb))/sqrt{ab}-((sqrta-sqrtb)(sqrta+sqrtb))/(sqrta-sqrtb)`
`=sqrta-sqrtb-(sqrta-sqrtb)`
`=-2sqrtb`
Đúng 1
Bình luận (0)
`(a\sqrtb-b\sqrta)/(\sqrt(ab)) -(a-b)/(\sqrta-\sqrtb)`
`=(\sqrt(ab) (\sqrta-\sqrtb))/(\sqrt(ab)) - ((\sqrta-\sqrtb)(\sqrta+\sqrtb))/(\sqrta-\sqrtb)`
`=(\sqrta-\sqrtb) - (\sqrta+\sqrtb)`
`=-2\sqrtb`
Đúng 1
Bình luận (0)
a)Cho A=x(x-4).Với giá trị nào của x thì :A=0;A<0;A>0
b)Cho B\(\frac{x-3}{x}\left(x\ne0\right)\).Với giá trị nào của x thì:B=0;B<0;B>
a)
Với A=0
\(\Rightarrow x\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)
với A<0
\(\Rightarrow x\left(x-4\right)< 0\)
\(th1\orbr{\begin{cases}x< 0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x>4\end{cases}\Leftrightarrow4< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x>0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x< 4\end{cases}\Leftrightarrow0< x< 4\left(tm\right)}\)
\(\Leftrightarrow0< x< 4\Leftrightarrow x\in\left\{1;2;3\right\}\)
Với A>0
\(\Rightarrow x\left(x-4\right)>0\)
\(th1\orbr{\begin{cases}x>0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x>4\end{cases}}\Leftrightarrow x>4\)
\(th2\orbr{\begin{cases}x< 0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x< 4\end{cases}}\Leftrightarrow x< 0\)
b)
Với B=0
\(\Rightarrow\frac{x-3}{x}=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\Rightarrow x=3\\x=0\left(l\right)\end{cases}}\)
vậy x=3 thì B = 0
Với B < 0
\(\Rightarrow\frac{x-3}{x}< 0\)
\(th1\orbr{\begin{cases}x-3>0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x< 0\end{cases}\Leftrightarrow3< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x-3< 0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x>0\end{cases}\Leftrightarrow0< x< 3\left(tm\right)\Leftrightarrow x\in\left\{1;2\right\}}\)
Với B > 0
\(th1\orbr{\begin{cases}x-3>0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x>0\end{cases}\Leftrightarrow x>3}\)
\(th2\orbr{\begin{cases}x-3< 0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 0\end{cases}\Leftrightarrow x< 0}\)





















