Lập phương trình bậc 2 có nghiệm X1,X2 thỏa x1+x2=4 và x12+x22 =10

Những câu hỏi liên quan
Cho phương trình
x
2
+
2
m
x
-
3
m
+
4
0
. Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
Đọc tiếp
Cho phương trình x 2 + 2 m x - 3 m + 4 = 0 . Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
![]()
![]()
![]()
![]()
Đáp án: D
Theo định lý Vi-ét ta có
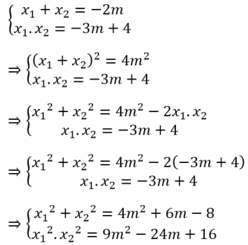
Khi đó, ![]() là nghiệm của phương trình
là nghiệm của phương trình
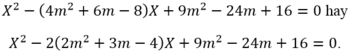
Đúng 0
Bình luận (0)
Cho phương trình bậc hai x 2 + 4x + m = 0 (1)
c) Xác định m để phương trình (1) có hai nghiệm x 1 và x 2 thỏa mãn x 1 2 + x 2 2 = 10.
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 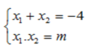
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10
Đúng 0
Bình luận (0)
Cho phương trỡnh bậc hai x2 + 5x + 3 = 0 có hai nghiệm x1; x2. Hãy lập một phương trình bậc hai cú hai nghiệm (x12 + 1 ) và ( x22 + 1)
cho phương trình bậc hai (m+2)x2 - 2(m-1)+3-m=0. Tìm m để phương trình có 2 nghiệm x1,x2 và thỏa mãn hệ thức x12 + x22 = x1+x2.
A. m∈(3;4) B. m∈(5;6) C. m∈(4;5) D. m∈(6;7)
đáp án đúng là A nhưng mà em không biết cách giải mọi người giúp với ạ
Điều kiện: \(m+2\ne0\Leftrightarrow m\ne-2\)
Ta có: \(\left(m+2\right)^2-2\left(m-1\right)x+3-m=0\)
\(\Rightarrow\Delta=4\left(m-1\right)^2-4\left(m+2\right)\left(3-m\right)\)
Để phương trình có hai nghiệm thì \(\Delta\ge0\)
\(\Rightarrow4\left(m^2-2m+1\right)-4\left(3m-m^2+6-2m\right)\ge0\)
\(\Leftrightarrow\left(m^2-2m+1\right)\ge\left(m-m^2+6\right)\)
\(\Leftrightarrow2m^2-3m-5\ge0\) \(\Leftrightarrow\left\{{}\begin{matrix}m\le-1\\m\ge\dfrac{5}{2}\end{matrix}\right.\)
Áp dụng định lí Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_1=\dfrac{2\left(m-1\right)}{m+2}\\x_1x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow\left(\dfrac{2\left(m-1\right)}{m+2}\right)^2-2\dfrac{3-m}{m+2}=\dfrac{2\left(m-1\right)}{m+2}\)
\(\Leftrightarrow\dfrac{4\left(m^2-2m+1\right)}{m^2+4m+4}=\dfrac{2m-2+6-2m}{m+2}\)
\(\Leftrightarrow\dfrac{4m^2-8m+4}{m^2+4m+4}=\dfrac{4}{m+2}\)
\(\Leftrightarrow\left(4m^2-8m+4\right)\left(m+2\right)=4m^2+16m+16\)
\(\Leftrightarrow\left(4m^3-8m^2+4m+8m^2-16m+8\right)=4m^2+16m+16\)
\(\Leftrightarrow\left(4m^3-4m^2-28m-8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m\approx3,3\\m\approx-0,3\left(loai\right)\end{matrix}\right.\)
Vậy m \(\in\left(3;4\right)\)
Câu A
Đúng 1
Bình luận (0)
Cho phương trình : x2-4x+m=0(m là tham số)
a) Tính các giá trị của m để phương trình có các nghiệm x1,x2 thỏa mãn x1< x2 và x22-x12=18
Lời giải:
Để pt có nghiệm thì $\Delta'=4-m\geq 0\Leftrightarrow m\leq 4$
Áp dụng hệ thức Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=4$
$x_1x_2=m$
Khi đó:
$x_2^2-x_1^2=18$
$\Leftrightarrow (x_2-x_1)(x_2+x_1)=18$
$\Leftrightarrow (x_2-x_1).4=18$
$\Leftrightarrow x_2-x_1=4,5$
$\Rightarrow (x_2-x_1)^2=20,25$
$\Leftrightarrow (x_2+x_1)^2-4x_1x_2=20,25$
$\Leftrightarrow 4^2-4m=20,25$
$\Leftrightarrow m=\frac{-17}{16}$ (tm)
Đúng 1
Bình luận (0)
Cho phương trình : x2 + 2mx + 2m - 2 = 0 ( * ) ( x là ẩn số ) . a ) Chứng tỏ phương trình ( * ) luôn có nghiệm x1 , x2 với mọi m . b ) Tìm giá trị tham số m để hai nghiệm x1, x2 của phương trình : ( * ) thỏa mãn : x12 + x22 - 3x1x2 = 4
Xem chi tiết
PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!
Đúng 0
Bình luận (1)
Lời giải:
a)
Ta có: $\Delta'=m^2-(2m-2)=m^2-2m+2=(m-1)^2+1>0$ với mọi $m\in\mathbb{R}$
Do đó pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m\in\mathbb{R}$
b)
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-2m\\ x_1x_2=2m-2\end{matrix}\right.\)
Để $x_1^2+x_2^2-3x_1x_2=4$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=4$
$\Leftrightarrow (-2m)^2-5(2m-2)=4$
$\Leftrightarrow 4m^2-10m+6=0$
$\Leftrightarrow 2m^2-5m+3=0$
$\Leftrightarrow (m-1)(2m-3)=0$
$\Rightarrow m=1$ hoặc $m=\frac{3}{2}$ (đều thỏa mãn)
Đúng 0
Bình luận (0)
Tìm các giá trị của m để phương trình
x
2
– 2mx + 2m − 1 0 có hai nghiệm
x
1
;
x
2
thỏa mãn
x
1
2
+
x
2
2
10
A. m −2 B. m 1 C. m −3 D. Cả A và B
Đọc tiếp
Tìm các giá trị của m để phương trình x 2 – 2mx + 2m − 1 = 0 có hai nghiệm x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 = 10
A. m = −2
B. m = 1
C. m = −3
D. Cả A và B
Phương trình x 2 – 2mx + 2m − 1 = 0 có a = 1 ≠ 0 và = 4 m 2 – 4 (2m – 1)
= 4 m 2 – 8 m + 4 = 4 ( m – 1 ) 2 ≥ 0 ; ∀ m
Phương trình có hai nghiệm x 1 ; x 2 với mọi m
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m x 1 . x 2 = 2 m − 1
Xét
x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 ⇔ 4 m 2 – 2 ( 2 m – 1 ) = 10
⇔ 4 m 2 – 4 m + 2 – 10 = 0 ⇔ 4 m 2 – 4 m – 8 = 0 ⇔ m 2 – m – 2 = 0
m 2 – 2 m + m – 2 = 0 ⇔ m ( m – 2 ) + ( m – 2 ) = 0 ⇔ ( m + 1 ) ( m – 2 ) = 0
⇔ m = 2 m = − 1
Vậy m = 2 và m = −1 là các giá trị cần tìm
Đáp án: D
Đúng 0
Bình luận (0)
Cho phương trình X2 -m -2X+2m-80 ( m là tham số)a) C/m phương trình luôn có nghiệm với mọi giá trị của mb) Tính S và P theo mc) Tìm m để phương trình có 2 nghiệm X1;X2 thỏa X12+X22-X1-X214
Đọc tiếp
Cho phương trình X2 -m -2X+2m-8=0 ( m là tham số)
a) C/m phương trình luôn có nghiệm với mọi giá trị của m
b) Tính S và P theo m
c) Tìm m để phương trình có 2 nghiệm X1;X2 thỏa X12+X22-X1-X2=14
Cho phương trình: x2 - (2m - n)x + (2m + 3n - 1) = 0 (m,n là tham số)
Tìm m,n để phương trình có hai nghiệm x1,x2 thỏa mãn x1 + x2 = -1 và x12 + x22 = 13
Giả sử pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-n\\x_1x_2=2m+3n-1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1^2+x_2^2=13\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-1\\\left(x_1+x_2\right)^2-2x_1x_2=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-n=-1\\2m+3n-1=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=-1\\m=-1\end{matrix}\right.\)
Đúng 5
Bình luận (0)
Cho phương trình ẩn x: x2 - 2(m+1)x + m2 - 1 = 0 . Tìm giá trị của m để phương tình có 2 nghiệm x1 x2 thỏa mãn x12 + x22 = x1.x2 + 8
Lời giải:
Để PT có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-(m^2-1)>0\Leftrightarrow 2m+2>0\Leftrightarrow m>-1$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$ và $x_1x_2=m^2-1$
Khi đó, để $x_1^2+x_2^2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2=3x_1x_2+8$
$\Leftrightarrow 4(m+1)^2=3(m^2-1)+8$
$\Leftrightarrow m^2+8m-1=0$
$\Leftrightarrow m=-4\pm \sqrt{17}$. Vì $m>-1$ nên $m=-4+\sqrt{17}$
Đúng 2
Bình luận (0)

















