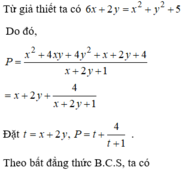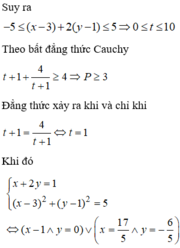Cho x ,y là 2 số thực thỏa mãn x^2 + 4y^4 = 1. CMr l x + y l =< căn 5 / 2

Những câu hỏi liên quan
1. Cho số thực x. CMR: \(x^4+5>x^2+4x\)
2. Cho số thực x, y thỏa mãn x>y. CMR: \(x^3-3x+4\ge y^3-3y\)
3. Cho a, b là số thực dương thỏa mãn \(a^2+b^2=2\). CMR: \(\left(a+b\right)^5\ge16ab\sqrt{\left(1+a^2\right)\left(1+b^2\right)}\)
Cho x,y là các số thực thỏa mãn:\(x,y\ge0\) và 1=x^2+y^2.CMR: 1/căn 2<= x^3+y^3<=1
Giúp mk với ạ.<= là nhỏ hơn hoặc bằng nha
Lời giải;
Vế 1:
Áp dụng BĐT AM-GM:
$2=(x^2+y^2)(1+1)\geq (x+y)^2\Rightarrow x+y\leq \sqrt{2}$
$x^3+\frac{x}{2}\geq \sqrt{2}x^2$
$y^3+\frac{y}{2}\geq \sqrt{2}y^2$
$\Rightarrow x^3+y^3+\frac{x+y}{2}\geq \sqrt{2}(x^2+y^2)=\sqrt{2}$
$\Rightarrow x^3+y^3\geq \sqrt{2}-\frac{x+y}{2}\geq \sqrt{2}-\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$
-----------------------
Vế 2:
$x^2+y^2=1$
$\Rightarrow x^2=1-y^2\leq 1\Rightarrow -1\leq x\leq 1$
$y^2=1-x^2\leq 1\Rightarrow -1\leq y\leq 1$
$\Rightarrow x^3\leq x^2; y^3\leq y^2$
$\Rightarrow x^3+y^3\leq x^2+y^2$ hay $x^3+y^3\leq 1$
Đúng 0
Bình luận (0)
cho x,y là các số thực dương phân biệt thỏa mãn
\(\frac{y}{x+y}+\frac{2y^2}{x^2+y^2}+\frac{4y^4}{x^4+y^4}+\frac{8y^8}{x^8-y^8}=4\)
CMR : 5y=4x
Giả sử : \(y=ax\)
Thay vào giả thiết : \(\frac{ax}{x+ax}+\frac{2\left(ax\right)^2}{x^2+\left(ax\right)^2}+\frac{4\left(ax\right)^4}{x^4+\left(ax\right)^4}+\frac{8\left(ax\right)^8}{x^8-\left(ax\right)^8}=4\)
\(\Leftrightarrow\frac{x.a}{x.\left(a+1\right)}+\frac{x^2.2a^2}{x^2\left(1+a^2\right)}+\frac{x^4.4a^4}{x^4\left(1+a^4\right)}+\frac{x^8.8a^8}{x^8\left(1-a^8\right)}=4\)
\(\Leftrightarrow\frac{a}{a+1}+\frac{2a^2}{a^2+1}+\frac{4a^4}{a^4+1}+\frac{8a^8}{1-a^8}=4\)
Tới đây bạn giải ra , tìm a rồi thay vào y = ax là ra :)
Đúng 1
Bình luận (0)
Cho 2 số thực x,y thỏa mãn: \(x^2+y^2=x\sqrt{1-y^2}+y\sqrt{1-x^2}\)CMR: 3x+4y\(\le5\)
Cho Các số thực dương x, y, z thỏa mãn x +y +z=9 (x>1, y>2, Z>3)
Cmr \(\frac{x}{y^2-4y+5}+\frac{y-1}{z^2-6z+10}+\frac{z-2}{x^2-2x+2}\ge3\)
1, tìm các số thực x,y thỏa mãn:\(\dfrac{x}{x^2+1}=y^2-4y+5\)
Ta có: \(\dfrac{x}{x^2+1}-\dfrac{1}{2}=\dfrac{-\left(x-1\right)^2}{x^2+1}\le0\)
\(\Rightarrow\dfrac{x}{x^2+1}\le\dfrac{1}{2}\) ;\(\forall x\)
Mặt khác: \(y^2-4y+5=\left(y-2\right)^2+1\ge1\)
\(\Rightarrow y^2-4y+5>\dfrac{x}{x^2+1}\) ; \(\forall x;y\)
\(\Rightarrow\) Không tồn tại x, y thỏa mãn yêu cầu đề bài
Đúng 2
Bình luận (0)
Cho x, y là các số thực thỏa mãn
(
x
−
3
)
2
+
(
y
−
1
)
2
5
. Giá trị nhỏ nhất của biểu thức
P
3
y
2
+...
Đọc tiếp
Cho x, y là các số thực thỏa mãn ( x − 3 ) 2 + ( y − 1 ) 2 = 5 . Giá trị nhỏ nhất của biểu thức P = 3 y 2 + 4 x y + 7 x + 4 y − 1 x + 2 y + 1 là
A. 2 3 .
B. 3 .
C. 114 11 .
D. 3
Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
Cho x, y là các số thực không âm thỏa mãn x+y=1
Chứng minh 1/căn 2<= x căn x+y căn y<= 1
Cho x,y là các số tự nhiên thỏa mãn 3x^2 + x= 4y^2 +y. Cmr 2xy +4(x+y)^3 +x^2+y^2 là số chính phương.
Giúp mik bài này nhé!!! cảm ơn nhiều:D