Em tham khảo câu a, b, c tại đây nhé.

Câu hỏi của Bảo Trân Nguyễn Hoàng - Toán lớp 7 - Học toán với OnlineMath

d) Ta thấy EB = AE

Mà theo quan hệ giữa đường vuông góc với đường xiên thì AC < AE

Vậy nên AC < EB.

a) Xét t/g vuông ACE và t/g vuông AKE ta có: 

gECA=gEKA=90^o

=>EA là cạnh huyền chung

Mà gCAE=gKAE( vì AE là tia p/g của góc A)

Nên t/gACE=t/gAKE(GH-GN)

=>AC=AK (2 cạnh tương ứng)

b)Lại có AC=AK (cmt)

=>A nằm trên đường trung trực của KC(1)

=>t/gAK=t/AE

=>E nằm trên đường trung trực của KC (2)

Từ (1)và (2) => AE là đường trung trực của KC

c)Ta có trong t/g vuông BCA thì 

gB+gA=90^o

=>gB-gA(90^o)-60^o=30^o

=>EAB=90^o

=>Ek vuông vs BA 

Mà cũng là đường trung trực của AEB

Nên KA=KB.

d) Thấy trong t/g vuông BEK : EB>EK

Mà KA=KB

KA=KC

=>BK=AC hay EB=AC

=>EB>EC

=>đpcm.

Hình sai sai

@dragon team vâng mình ngu hình lắm ạ :< nên cũng chẳng chắc vầy nên có j sai mong cậu bảo:Đ

a) Xét \(\Delta ACE\) và \(\Delta AKE\) có:

\(\left\{{}\begin{matrix}\widehat{ACE}=\widehat{AKE}=90^o\\AE-\text{cạnh chung}\\\widehat{EAC}=\widehat{EAK}\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow \Delta ACE=\Delta AKE(ch-gn)\)

b) Từ câu a ta có \(\Delta ACE=\Delta AKE\) nên AC = AK, EC = EK. Suy ra AE là đường trung trực của CK.

c) Đề bài sai

d) Ta có EK = EC mà EK < EB (quan hệ giữa đường vuông góc và đường xiên) nên EB > EC.

a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có

AE chung

góc CAE=góc KAE

=>ΔACE=ΔAKE

=>AC=AK và EC=EK

=>AE là trung trực của CK

b: Xét ΔEAB có góc EAB=góc EBA

nên ΔEAB cân tại E

mà EK là đường cao

nên K là trung điểm của AB

=>KA=KB

c: EB=EA

EA>AC

=>EB>AC

d: Gọi giao của BD và AC là M

Xét ΔAMB có

AD,BC là đường cao

AD cắt BC tại E

=>E là trực tâm

=>MD vuông góc AB

mà EK vuông góc AB

nên M,E,K thẳng hàng

=>AC,DB,EK đồng quy

a: \(\widehat{ABC}=30^0\)

b: Xét ΔACE vuông tại C và ΔAKE vuông tại K có

AE chung

\(\widehat{CAE}=\widehat{KAE}\)

Do đó: ΔACE=ΔAKE

c: Ta có: ΔACE=ΔAKE

nên AC=AK; EC=EK

hay AE là đường trung trực của CK

d: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)

nên ΔEAB cân tại E

mà EK là đường cao

nên K là trung điểm của AB

hay KA=KB

a) Xét tam giác ACE và tam giác AKE

có AE chung

góc CAE =góc KAE (GT)

góc ECA = góc EKA =90⁰

suy ra tam giác ACE = tam giác AKE (cạnh huyền-góc nhọn) (1)

b) Từ (1) suy ra AC=AK suy ra A thuộc đường trung trực của CK  (2)

Từ (1) suy ra EK=EC suy ra E thuộc đường trung trực của CK  (3)

Từ(2) và (3) suy ra AE là  đường trung trực của CK

c) tam giác ABC vuông tại C, có góc CAB = 60⁰

suy ra AC=AB:2 ( cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)

mà AK=AC , AK +KB=AB

suy ra AK=AC=KB

d) tam giác BDE=tam giác BKE (cạnh huyền-góc nhọn)

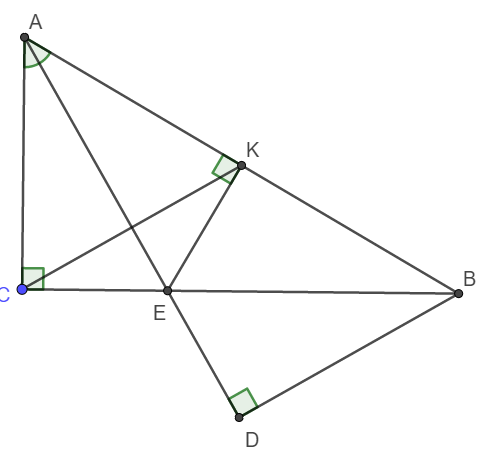
a) Xét tam giác vuông ACE và tam giác vuông AKE có:

Cạnh AE chung

\(\widehat{CAE}=\widehat{KAE}\)  (gt)

\(\Rightarrow\Delta ACE=\Delta AKE\)    (Cạnh huyền - góc nhọn)

b) Do \(\Delta ACE=\Delta AKE\) nên AC = AK hay tam giác ACK cân tại A.

Vậy thì phân giác AE cũng đồng thời là đường trung trực của CK.

c) Xét tam giác ABC vuông có góc \(\widehat{CAB}=60^o\Rightarrow\widehat{CBA}=30^o\)

Xét tam giác AEB có \(\widehat{EAB}=\widehat{ABE}\left(=30^o\right)\) nên AEB là tam giác cân tại E.

Vậy thì đường cao EK đồng thời là trung tuyến hay KA = KB.