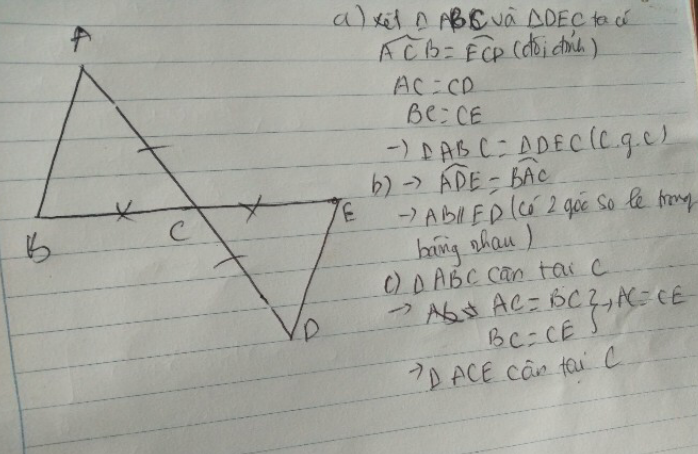1/ Cho ΔABC; trên cạnh AB lấy điểm D và E sao cho AD=BE. Qua D và E kẻ các đường thẳng song song với BC chúng cắt AC theo thứ tự ở M và N. Chứng minh rằng: DM+EN=BC

Những câu hỏi liên quan
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng kdfrac{3}{2} . Diện tích ΔABC là 27 cm^2, thi diện tích ΔDEF là:A. 12cm^2 B.24cm^2 C. 36cm^2 D. 18cm^22) ΔABC ∼ΔDEF có AB3cm, AC5cm, BC7cm, DE6cm. Ta có :A. DF10cm B. DF20cm C. EF14cm D.EF10cm
Đọc tiếp
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng k=\(\dfrac{3}{2}\) . Diện tích ΔABC là 27 cm\(^2\), thi diện tích ΔDEF là:
A. 12cm\(^2\) B.24cm\(^2\) C. 36cm\(^2\) D. 18cm\(^2\)
2) ΔABC ∼ΔDEF có AB=3cm, AC=5cm, BC=7cm, DE=6cm. Ta có :
A. DF=10cm B. DF=20cm C. EF=14cm D.EF=10cm
Xem thêm câu trả lời
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)
ΔABC. Trên tia đối của tia AB lấy điểm Đ sao cho AD = \(\dfrac{1}{3}\)AB. Trên tia đối của tia AC lấy điểm E sao cho AE = \(\dfrac{1}{3}\)AC. C/minh : ΔADE đồng dạng với ΔABC, tìm tỉ số đồng dạng?
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{3}\right)\)
\(\widehat{DAE}=\widehat{BAC}\)(hai góc đối đỉnh)
Do đó: ΔADE\(\sim\)ΔABC(c-g-c)
Suy ra: \(k=\dfrac{AD}{AB}=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
cho ΔABC và ΔDEF có AB=EF và BC=DE
A) Muốn ΔABC và ΔDEF bằng nhau theo trường hợp c_g_c thì cần thiếu điều kiện nào( đủ 1 điều kiện)
B) giả sữ ΔABC có góc c= 54 độ; AC= 6cm. Tính số đo của cạnh góc tương ứng trong ΔDEF
a: \(\widehat{B}=\widehat{E}\)
Đúng 0
Bình luận (0)
1. Cho ΔABC cân tại A: K,H ϵ AB, AC sao cho AK= AH. C/m BK=CK
2. ΔABC cân tại A. Kẻ BH, CK sao cho K, H ϵ AB, AC và góc HBC= góc KCB. C/m góc ABH = góc ACK
2: góc ABH+góc HBC=góc ABC
góc ACK+góc KCB=góc ACB
mà góc ABC=góc ACB; góc HBC=góc KCB
nên góc ABH=góc ACK
Đúng 1
Bình luận (0)
a)Cho ΔABC có a=5,b=6,góc ACB=30 độ.Tính cạnh AB
b)Cho ΔABC cân tại A,có cạnh AB=a.Tính số đo các cạnh,các góc còn lại của ΔABC và tính bán kính đường tròn ngoại tiếp ΔABC biết góc A=70 độ
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC. Lấy điểm D, E sao cho C là trung điểm của BE và AD. Chứng minh:
a) ΔABC = ΔDEC; b) AB // DE
c) Nếu ΔABC cân tại C thì ΔAEC là tam giác gì? Vì sao?
Cho ΔABC, điểm M(-1/2 ; 3/2) là trung điểm AB. H(-2;4) là chân đường cao BH, I(-1;1) là tâm đường tròn ngoại tiếp ΔABC. Tìm tọa độ điểm C?
Cho ΔABC có AB=2; BC=3;AC=6 a) Tính diện tích ΔABC=? b) Tính độ dài đường trung tuyến kẻ từ C c) Tính bán kính đường tròn ngoại tiếp ΔABC d) Tính số đo góc lớn nhất trong ΔABC.
AB+BC<AC
nên ko có tam giác ABC thỏa mãn nha bạn
Đúng 2
Bình luận (0)