tìm khoảng đồng biến và nghịch biến của hàm số y = g(x) = f(2x-4)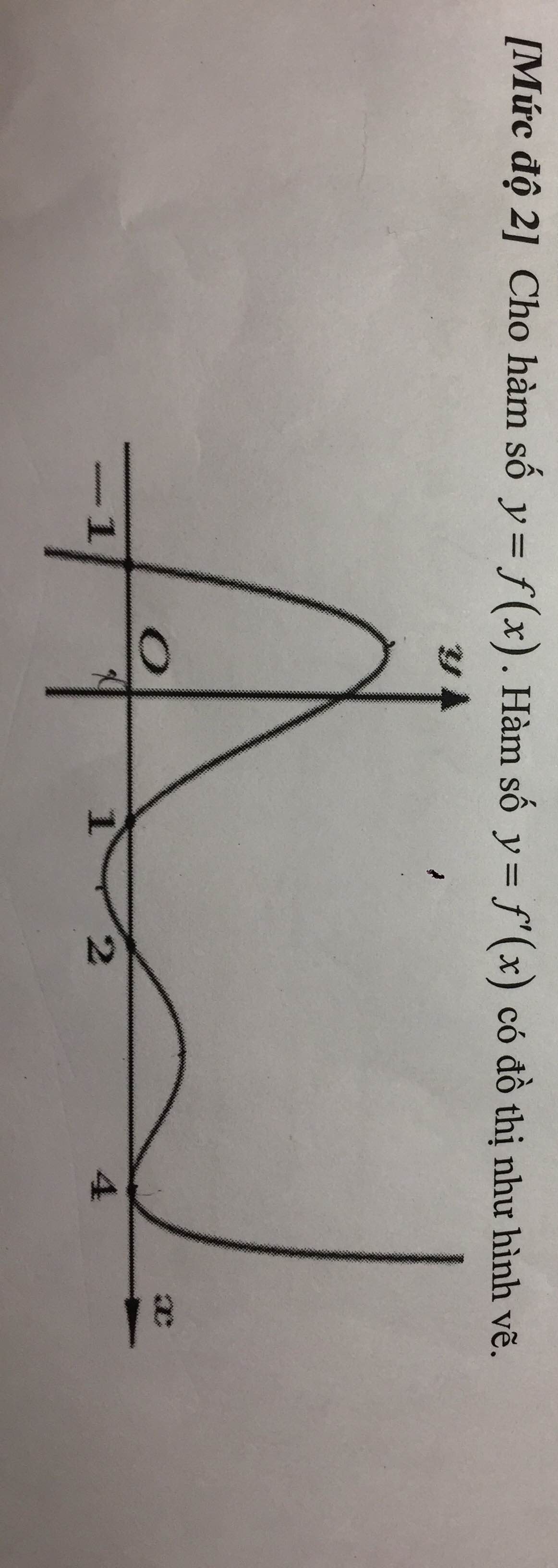

Những câu hỏi liên quan
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)
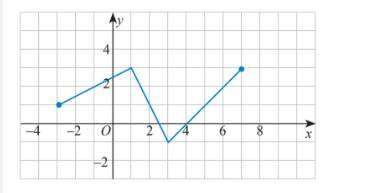
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Đúng 0
Bình luận (1)
cho hàm số y=f(x) có đạo hàm f'(x)= (x-1)(2x-3). Tìm khoảng đồng biến, nghịch biến
\(y=f\left(x\right)=\left(x-1\right)\left(2x-3\right)\) đồng biến khi: \(\left(x-1\right)\left(2x-3\right)>0\)
\(\Leftrightarrow x-1>0;2x-3>0\) hoặc \(x-1< 0;2x-3< 0\)
\(\Leftrightarrow x>1;x>\frac{3}{2}\) hoặc \(x< 1;x< \frac{3}{2}\)
\(\Leftrightarrow x>\frac{3}{2}\) hoặc \(x< 1\)
\(y=f\left(x\right)=\left(x-1\right)\left(2x-3\right)\) nghịch biến khi: \(\left(x-1\right)\left(2x-3\right)< 0\)
\(\Leftrightarrow x-1>0;2x-3< 0\) hoặc \(x-1< 0;2x-3>0\)
\(\Leftrightarrow x>1;x< \frac{3}{2}\) hoặc \(x< 1;x>\frac{3}{2}\)
\(\Leftrightarrow1< x< \frac{3}{2}\)
Tìm khoảng đồng biến và nghịch biến của hàm số y = \(\dfrac{x+3}{2x-5}\)
TXĐ: \(x\ne\dfrac{5}{2}\)
\(y'=\dfrac{-11}{\left(2x-5\right)^2}< 0,\forall x\ne\dfrac{5}{2}\)
=> hàm số nghịch biến trên khoảng (-vô cực; 5/2) và (5/2;+ vô cực)
Đúng 1
Bình luận (1)
hoặc bạn có thể dùng cách 2 :
TXĐ x≠5/2
rồi bạn lập tỉ số \(A=\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\)
+ nếu A>0 thì hs đb trên TXĐ
+ nếu A<0 thì hs nb trên TXĐ
P/s :ở đây theo mình nghĩ là A<0 nơi á :"))
Đúng 1
Bình luận (0)
Cho hàm số y f(x) có đồ thị của hàm số y f (x) được cho như hình bên và các mệnh đề sau: (1). Hàm số y f(x) đồng biến trên khoảng (-1;0) (2). Hàm số y f(x) nghịch biến trên khoảng (1;2) (3). Hàm số y f(x) đồng biến trên khoảng (3;5) (4). Hàm số y f(x) có hai điểm cực đại và một điểm cực tiểu.Số mệnh đề đúng là A. 1 B. 3 C. 4 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: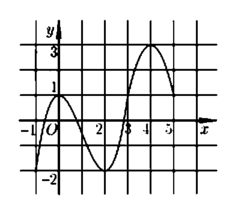
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
Đúng 0
Bình luận (0)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Đúng 2
Bình luận (0)
Khoảng nghịch biến của hàm số y= 1/2x^4-3x^2-3 là gì các bạn?
Hàm số y= x^2/1-x đồng biến trên khoảng nào?
Hàm số y= x^3+3x^2 nghịch biến trên khoảng nào?





















