Giải mình Câu 2 ạ

Những câu hỏi liên quan
Giải giúp mình 2 ảnh này với ạ (đặt câu hỏi ạ)


6 How often does your grandfather often listen to the radio
7 How often do you go to the gym
8 What did they send
9 What time did he leave the party
10 Where did he go
11 Who did he meet for coffee
12 Why did she called the firemen
13 How did he go to school
14 What does lan like doing
15 Where was your father last months
16 How much is the dictionary
17 How long did it take to finish the composition
18 Who bought a poster
What did Mrs Robinson by
19 Where is a restaurant
20 What did her neighbor give her
21 How was the homework yesterday
22 Do you have magaazine and newspapers
23 How often do you go to the movies
Đúng 1
Bình luận (4)
Giúp mình giải câu 2 với ạ
Giải giúp mình câu 2 với ạ 
Câu 2
a) nH2 = \(\dfrac{4,48}{22,4}=0,2mol\)
nancol = 2nH2 = 0,4 mol
=> Mancol = \(\dfrac{17}{0,4}=42,5\)
=> Hai ancol là CH3OH và C2H5OH
b) số ete thu được tối đa = \(\dfrac{n\left(n+1\right)}{2}\)
= \(\dfrac{2.3}{2}=3\)
Đúng 3
Bình luận (0)
Giải dùm mình 2 câu này với ạ
Đọc tiếp
Giải dùm mình 2 câu này với ạ![]()
5.
ĐKXĐ: \(cos\left(x-30^0\right)\ne0\Leftrightarrow x\ne120^0+k180^0\)
Pt tương đương:
\(\left[{}\begin{matrix}tan\left(x-30^0\right)=0\\cos\left(2x-150^0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-30^0=k180^0\\2x-150^0=90^0+k180^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=30^0+k180^0\\x=120^0+k90^0\end{matrix}\right.\)
Kết hợp ĐKXĐ: \(\Rightarrow x=30^0+k180^0\)
Đúng 2
Bình luận (0)
6.
\(\Leftrightarrow2\sqrt{2}sinx.cosx+2cosx=0\)
\(\Leftrightarrow2cosx\left(\sqrt{2}sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k2\pi\\x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
5. \(\Leftrightarrow\left[{}\begin{matrix}\tan\left(x-30\right)=0\\\cos\left(2x-150\right)=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-30=360k\\\left[{}\begin{matrix}2x-150=90+360k\\2x-150=270+360k\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=30+360k\\x=120+180k\\x=210+180k\end{matrix}\right.\)
Vậy ...
6, \(\Leftrightarrow2\sqrt{2}\sin x.\cos x+2\cos x=0\)
\(\Leftrightarrow\cos x\left(1+\sqrt{2}\sin x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=0\\\sqrt{2}\sin x+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{3}{2}\pi+k2\pi\end{matrix}\right.\\x=-\dfrac{\pi}{4}+k2\pi\\x=\dfrac{7}{4}\pi+k2\pi\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Giải hộ mình 2 câu đó với ạ 
6.
\(\Leftrightarrow x^2+4x+3>m\) ; \(\forall x>1\)
\(\Leftrightarrow m< \min\limits_{x>1}\left(x^2+4x+3\right)\)
Xét hàm \(f\left(x\right)=x^2+4x+3\) với \(x>1\)
\(-\dfrac{b}{2a}=-2< 1\) ; \(f\left(1\right)=8\Rightarrow f\left(x\right)>8\) ; \(\forall x>1\)
\(\Rightarrow m\le8\)
7.
Do C thuộc d nên tọa độ có dạng: \(C\left(-2c-1;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;6\right)\\\overrightarrow{CA}=\left(2c;1-c\right)\end{matrix}\right.\)
\(AB\perp AC\Leftrightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\Leftrightarrow4.2c+4\left(1-c\right)=0\)
\(\Leftrightarrow4c+4=0\Rightarrow c=-1\Rightarrow C\left(1;-1\right)\)
b.
\(AB=\sqrt{4^2+6^2}=2\sqrt{13}\)
Phương trình đường thẳng AB qua A và nhận \(\left(3;-2\right)\) là 1 vtpt có dạng:
\(3\left(x+1\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y+5=0\)
Do d thuộc d nên tọa độ có dạng: \(D\left(-2d-1;d\right)\)
\(S_{ABD}=\dfrac{1}{2}AB.d\left(D;AB\right)=50\)
\(\Leftrightarrow\dfrac{\sqrt{13}\left|3\left(-2d-1\right)-2d+5\right|}{\sqrt{3^2+\left(-2\right)^2}}=50\)
\(\Leftrightarrow\left|-8d+2\right|=50\Rightarrow\left[{}\begin{matrix}d=-6\\d=\dfrac{13}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}D\left(11;-6\right)\\D\left(-14;\dfrac{13}{2}\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
a, Gọi \(C=\left(-2m-1;m\right)\) là điểm cần tìm
\(AB=2\sqrt{13};AC=\sqrt{5m^2-2m+1};BC=\sqrt{5m^2+2m+65}\)
Ta có \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow5m^2+2m+65=52+5m^2-2m+1\)
\(\Leftrightarrow m=-3\)
\(\Rightarrow C=\left(5;-3\right)\)
b, Gọi \(D=\left(-2n-1;n\right)\) là điểm cần tìm
Đường thẳng AB có phương trình \(\dfrac{x+1}{4}=\dfrac{y-1}{6}\Leftrightarrow3x-2y+5=0\)
Khoảng cách từ \(D\) đến \(AB\):
\(d\left(D;AB\right)=\dfrac{\left|3\left(-2n-1\right)-2n+5\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|-8n+2\right|}{\sqrt{13}}\)
\(S_{ABC}=\dfrac{1}{2}.\dfrac{\left|-8n+2\right|}{\sqrt{13}}.2\sqrt{13}=50\)
\(\Rightarrow\left|4n-1\right|=25\)
\(\Leftrightarrow\left[{}\begin{matrix}n=-6\\n=\dfrac{13}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}N=\left(11;-6\right)\\N=\left(-14;\dfrac{13}{2}\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải câu 2:
mình cảm ơn nhiều ạ.

ĐỔi 30 phút =0,5 h
a,Vận tốc của người đó
\(v=\dfrac{s}{t}=\dfrac{5}{0,5}=10\left(\dfrac{km}{h}\right)\)
b,Chọn gốc tọa độ O trùng điểm cách A 1km và nằm trong AB
Chiều dương trục Ox : từ A đến B
Phương trình chuyển động của mỗi vật:
\(x_1=1+10t(km,h)\)
Đúng 1
Bình luận (0)
Giải giúp mình câu 1, 2 với ạ. 
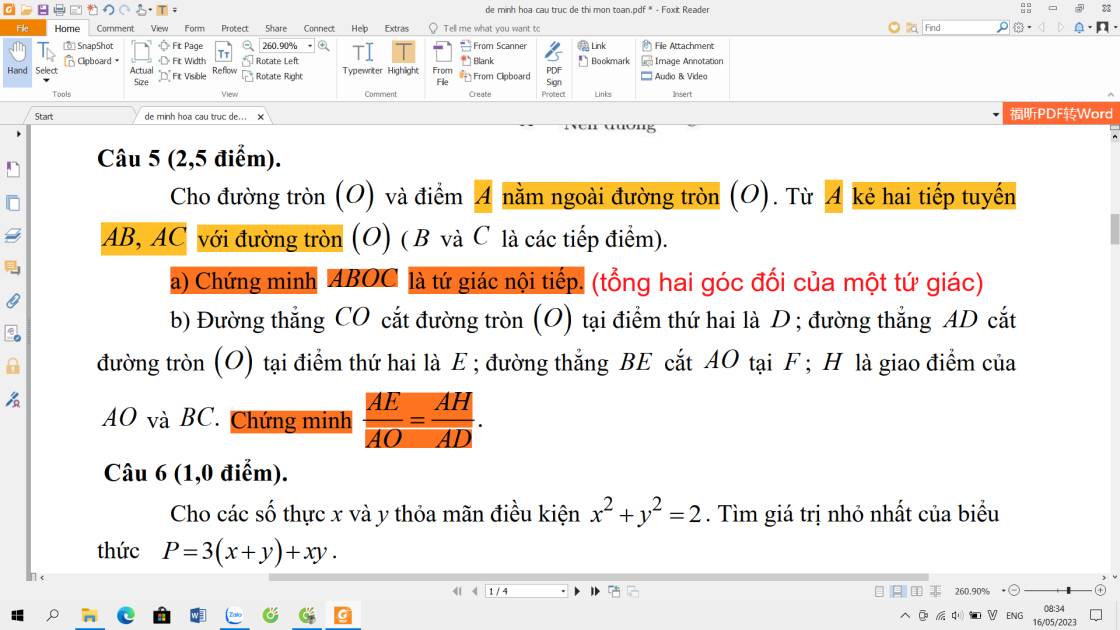 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ
5:
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD
Xet (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AH*AO=AB^2=AE*AD
=>AE/AO=AH/AD
Đúng 0
Bình luận (1)
Giúp mình giải câu 2 này với ạ
\(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
PTHH:
Zn + 2HCl ---> ZnCl2 + H2
0,1<-0,2<----------------0,1
\(n_{ZnO}=\dfrac{10,55-0,1.65}{81}=0,05\left(mol\right)\)
ZnO + 2HCl ---> ZnCl2 + H2
0,05-->0,1
\(C_{M\left(HCl\right)}=\dfrac{0,1+0,2}{0,2}=1.5M\)
Đúng 3
Bình luận (1)






















