Lời giải:

a.

PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$

Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$

Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.

b.

$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.

Vậy pt vô nghiệm.

c.

$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý

Vậy pt vô nghiệm

d.

$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$

Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý

Vậy pt vô nghiệm.

a, TK: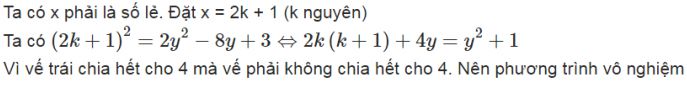

(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)

\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)

Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương

\(\dfrac{2-x}{2017}+1=\dfrac{x-1}{2018}-1+1-\dfrac{x}{2019}\)

\(\Leftrightarrow\dfrac{2019-x}{2017}=\dfrac{x-2019}{2018}+\dfrac{2019-x}{2019}\)

\(\Leftrightarrow\dfrac{2019-x}{2017}+\dfrac{2019-x}{2018}-\dfrac{2019-x}{2019}=0\)

\(\Leftrightarrow\left(2019-x\right)\left(\dfrac{1}{2017}+\dfrac{1}{2018}-\dfrac{1}{2019}\right)=0\)

\(\Leftrightarrow2019-x=0\) (do \(\dfrac{1}{2017}>\dfrac{1}{2019}\Rightarrow\dfrac{1}{2017}+\dfrac{1}{2018}-\dfrac{1}{2019}>0\))

\(\Rightarrow x=2019\)

Đặt t=\(\sqrt{2019-x^{ }2}\)>0, nên \(t^2\)=2019-\(x^2\) hay \(x^2\)=2019-\(t^2\).

từ đề bài ta có: 2019-\(t^2\)-\(t^2\)-2017t=0

hay 2\(t^2\)+2017t-2019=0, nên t=1 và t=-2019/2<0 loại

t=1, nên \(x^2\)=2018, nên x=2018 hoặc x=-2018 thỏa điều kiện 2019-\(x^2\)>=0

\(\frac{2-x}{2017}-1=\frac{1-x}{2018}-\frac{x}{2019}\)

\(\Leftrightarrow\) \(\frac{2-x}{2017}+1=\frac{1-x}{2018}+1-\frac{x}{2019}+1\)

\(\Leftrightarrow\) \(\frac{2019-x}{2017}=\frac{2019-x}{2018}-\frac{2019-x}{2019}\)

\(\Leftrightarrow\) \(\frac{2019-x}{2017}-\frac{2019-x}{2018}+\frac{2019-x}{2019}=0\)

\(\Leftrightarrow\) \(\left(2019-x\right)\left(\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2019}\right)=0\)

Mà \(\left(\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2019}\right)\ne0\)

\(\Rightarrow\) \(2019-x=0\) \(\Leftrightarrow\) \(x=2019\)

\(\Rightarrow\) \(S=\left\{2019\right\}\)

\(\dfrac{2-x}{2017}-1=\dfrac{1-x}{2018}-\dfrac{x}{2019}\Leftrightarrow\left(\dfrac{2-x}{2017}+1\right)=\left(\dfrac{1-x}{2018}+1\right)+\left(1-\dfrac{x}{2019}\right)\)

\(\Leftrightarrow\dfrac{2019-x}{2017}=\dfrac{2019-x}{2018}+\dfrac{2019-x}{2019}\)\(\Leftrightarrow\left(2019-x\right)\left(\dfrac{1}{2017}-\dfrac{1}{2018}-\dfrac{1}{2019}\right)=0\)

Ta đã có: \(\dfrac{1}{2017}-\dfrac{1}{2018}-\dfrac{1}{2019}< 0\)

Vậy ta dễ dàng suy ra được \(S=\left\{2019\right\}\)

Cố gắng học Thư nhé! Say oh yeah!