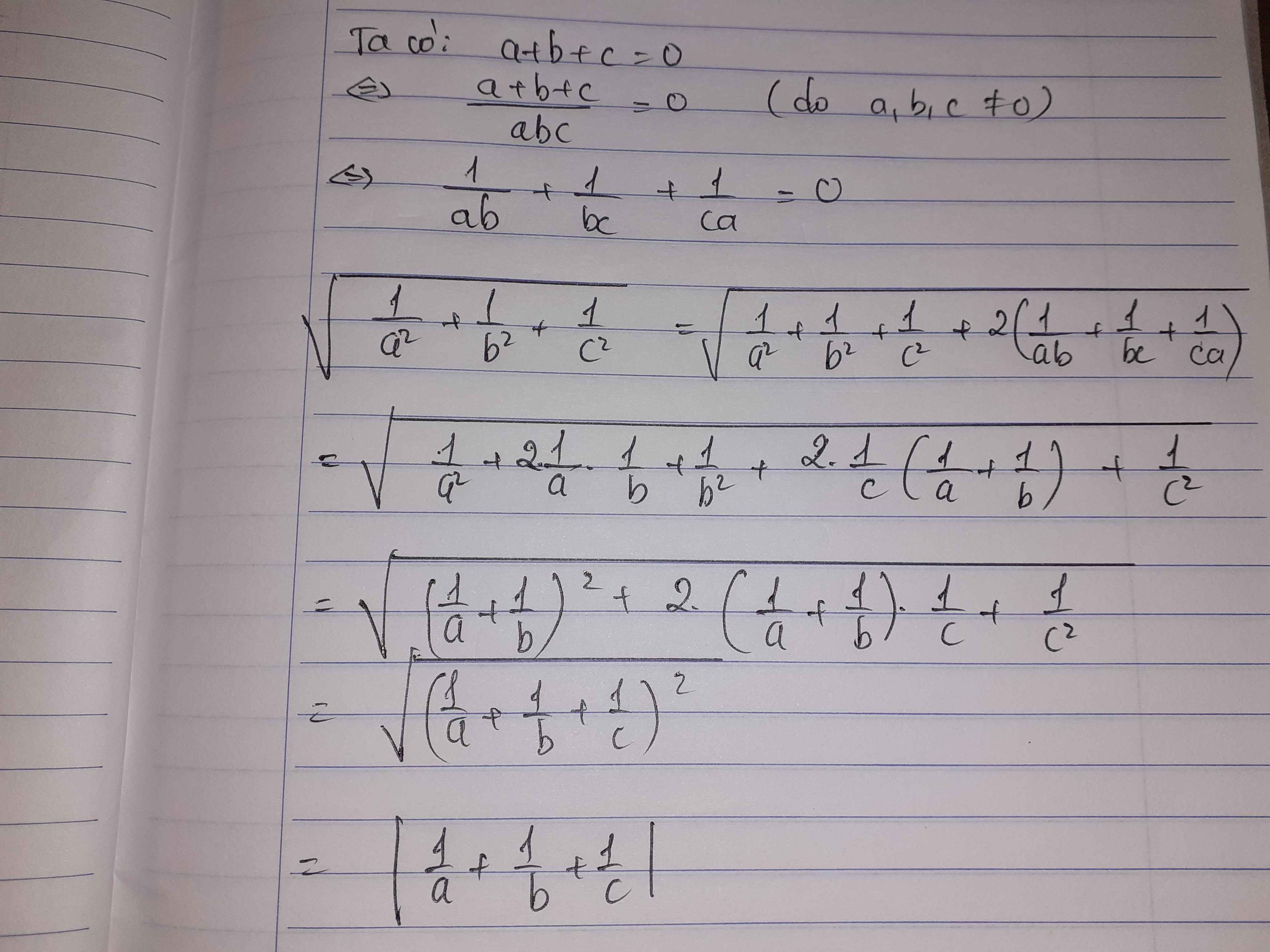Nếu \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{a+b}\) (với a,b\(\ne\)0; a\(\ne\)-b) thì giá trị của biểu thức \(\dfrac{b}{a}+\dfrac{a}{b}\) là:........

Những câu hỏi liên quan
CM nếu \(\dfrac{1}{a}\)+\(\dfrac{1}{b}\)+\(\dfrac{1}{c}\)=2 và a+b+c=abc
thì \(\dfrac{1}{a^2}\)+\(\dfrac{1}{b^2}\)+\(\dfrac{1}{c^2}\)=2 (a,b,c ≠ 0 và a+b+c ≠ 0)
Cho hai mặt phẳng (P): ax+2y-az+1=0 và (Q): 3x-(b+1)y+2z-b=0. Tìm hệ thứcliên hệ giữa a và b để (P) và (Q) vuông góc với nhau.
A. a-2b-2=0
B. 2a-b=0
C. \(\dfrac{a}{3}=\dfrac{2}{-\left(b+1\right)}=\dfrac{-a}{2}\ne\dfrac{1}{-b}\)
D. \(\dfrac{a}{3}\ne\dfrac{2}{-\left(b+1\right)}\ne\dfrac{-a}{2}\ne\dfrac{1}{-b}\)
Với bne0;bne-1b0;b−1 , tổng dfrac{a}{b}+dfrac{-a}{b+1}ba+b+1−a bằng:
Đọc tiếp
Với , tổng bằng:
Cho \(\dfrac{1}{c}=\dfrac{1}{2}.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)(với a,b,c \(\ne\)0, b \(\ne\)c) . Chứng minh rằng \(\dfrac{a}{b}=\dfrac{a-c}{c-b}\)
\(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\)
\(\frac{1}{c}:\frac{1}{2}=\frac{1}{a}+\frac{1}{b}\)
\(\frac{2}{c}=\frac{a+b}{ab}\)
\(\Rightarrow2ab=ac+bc\)
\(\Rightarrow ac-ab=ab-bc\)
\(\Rightarrow a.\left(c-b\right)=b.\left(a-c\right)\)
\(\Rightarrow\frac{a}{b}=\frac{a-c}{c-b}\)( đpcm )
Đúng 0
Bình luận (0)
oOo Thiếu gia ác ma đừng hôn tôi oOo có gì ko
Đúng 0
Bình luận (0)
Đưa các biểu thức sau thành phân thức:
a) M=\(\dfrac{\dfrac{y}{4}-2+\dfrac{15}{4y}}{\dfrac{y}{2}+\dfrac{6}{y}-\dfrac{7}{2}}\) với y \(\ne\) 0; y \(\ne\) 3 và y \(\ne\) 4
b) N=\(\dfrac{3b-\dfrac{1}{9b^2}}{1+\dfrac{1}{3b}+\dfrac{1}{9b^2}}\) với b \(\ne\) 0
Giúp mình với.
a) Cho các số a, b, c thỏa mãn abc\(\ne\) 0 và \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) =\(\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{a+c}{b}\)=\(\dfrac{1}{3}\). Tính S= a + b + c + 2021.
Cho a + b + c = 0; a,b,c \(\ne\) 0
Chứng minh đa thức \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\left|\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right|\)
Ta có: \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\left(\dfrac{c}{abc}+\dfrac{b}{abc}+\dfrac{a}{abc}\right)}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\cdot\dfrac{a+b+c}{abc}}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Đúng 2
Bình luận (0)
Cho a,b,c≠0 thỏa mán a+b+c=0.Chứng minh rằng:
\(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\)
Cho a,b,c\(\ne\)0 thỏa a+b+c=0 thì
\(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
Ta có: \(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
\(=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}\)
Ta cần chứng minh: \(\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}=0\) thật vậy:
\(\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}=\dfrac{2\left(a+b+c\right)}{abc}=\dfrac{2.0}{abc}=0\)Tức là:\(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\left(đpcm\right)\)
Đúng 0
Bình luận (0)