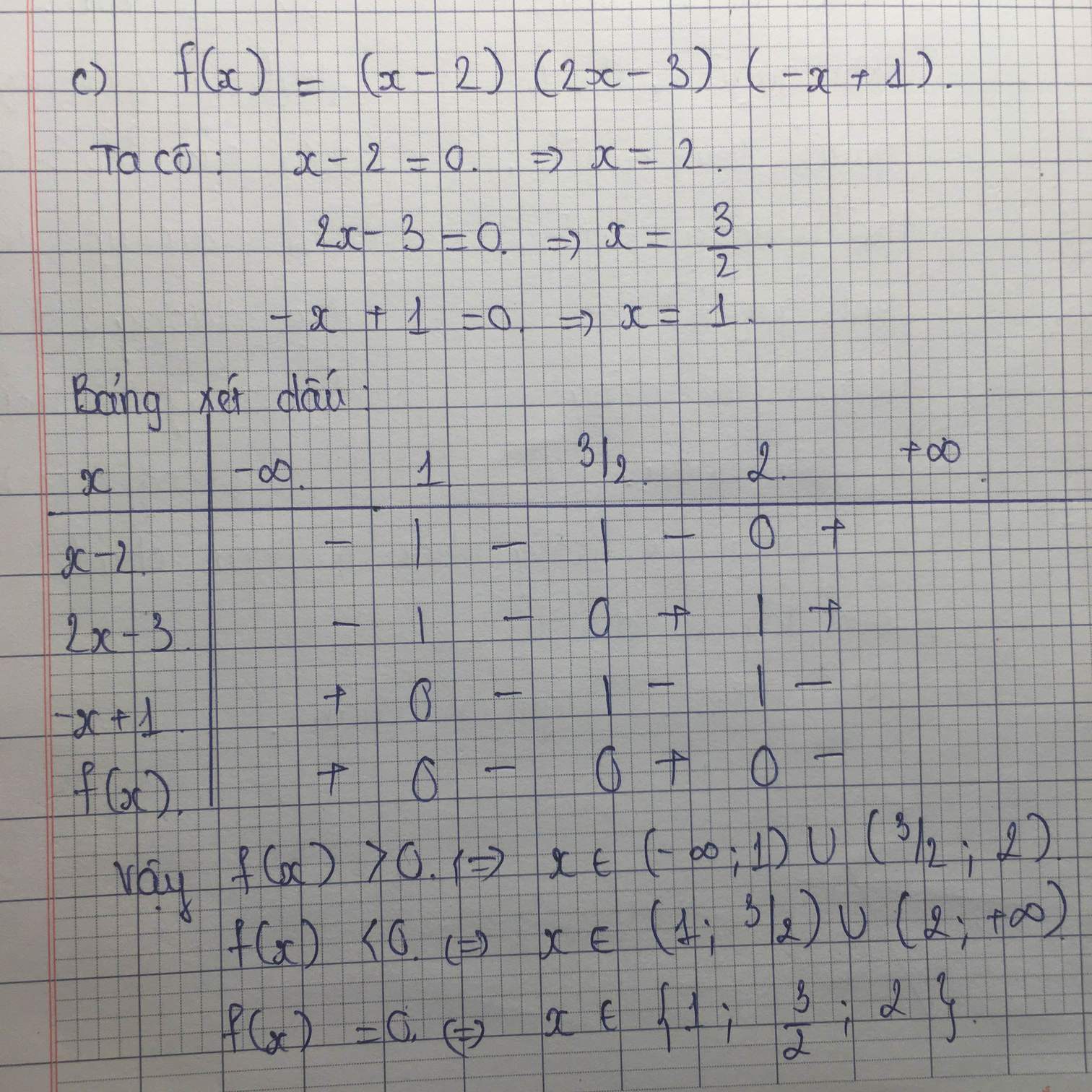Giúp em câu a với câu b với 

Những câu hỏi liên quan
Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.Lời giải câu a,b,c của em:
Đọc tiếp

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Đọc tiếp
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Câu a : A là Na B là K
Giúp em câu B với ạ !!!
Giúp em câu a, b, c câu 2 với ạ (•ө•)♡
b: \(\Leftrightarrow x\sqrt{2}=2\sqrt{2}+5\sqrt{2}=7\sqrt{2}\)
hay x=7
Đúng 1
Bình luận (0)
Giúp em câu b với câu d với ạ.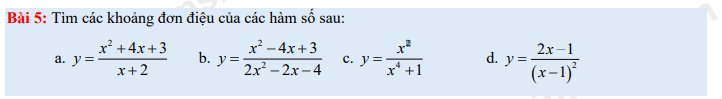
b: ĐKXĐ: \(2x^2-2x-4<>0\)
=>\(x^2-x-2<>0\)
=>(x-2)(x+1)<>0
=>x∉{2;-1}
Ta có: \(y=\frac{x^2-4x+3}{2x^2-2x-4}\)
=>\(y^{\prime}=\frac{\left(x^2-4x+3\right)^{\prime}\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(2x^2-2x-4\right)^{\prime}}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{\left(2x-4\right)\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(4x-2\right)}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{4x^3-4x^2-8x-8x^2+8x+16-\left(4x^3-2x^2-16x^2+8x+12x-6\right)}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{4x^3-12x^2+16-\left(4x^3-18x^2+20x-6\right)}{\left(2x^2-2x-4\right)^2}=\frac{6x^2-20x+22}{\left(2x^2-2x-4\right)^2}\)
Đặt y'>0
=>\(6x^2-20x+22>0\)
=>\(3x^2-10x+11>0\)
=>\(x^2-\frac{10}{3}x+\frac{11}{3}>0\)
=>\(x^2-\frac{10}{3}x+\frac{25}{9}+\frac{11}{3}-\frac{25}{9}>0\)
=>\(\left(x-\frac53\right)^2+\frac89>0\) (luôn đúng)
=>Hàm số đồng biến trên các khoảng xác định của nó
=>Hàm số đồng biến trên các khoảng (-∞;-1); (-1;2); (2;+∞)
d: \(y=\frac{2x-1}{\left(x-1\right)^2}\) (ĐKXĐ: x<>1)
=>\(y=\frac{2x-1}{x^2-2x+1}\)
=>\(y^{\prime}=\frac{\left(2x-1\right)^{\prime}\left(x^2-2x+1\right)-\left(2x-1\right)\left(x^2-2x+1\right)^{\prime}}{\left(x^2-2x+1\right)^2}\)
=>\(y^{\prime}=\frac{2\left(x^2-2x+1\right)-\left(2x-1\right)\left(2x-2\right)}{\left(x^2-2x+1\right)^2}=\frac{2x^2-4x+2-\left(4x^2-6x+2\right)}{\left(x^2-2x+1\right)^2}\)
\(=\frac{2x^2-4x+2-4x^2+6x-2}{\left(x^2-2x+1\right)^2}=\frac{-2x^2+2x}{\left(x^2-2x+1\right)^2}=\frac{-2x\left(x-1\right)}{\left(x^2-2x+1\right)^2}\)
Đặt y'<0
=>-2x(x-1)<0
=>x(x-1)>0
=>\(\left[\begin{array}{l}x>1\\ x<0\end{array}\right.\)
=>Hàm số nghịch biến trên các khoảng (1;+∞) và (-∞;0)
Đặt y'>0
=>-2x(x-1)>0
=>x(x-1)<0
=>0<x<1
=>Hàm số đồng biến trên khoảng (0;1)
Đúng 0
Bình luận (0)
Giúp em câu A với câu C giải nhanh giúp em ạ 
a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)
Đúng 0
Bình luận (0)
Ai giúp em giải câu b, c, d với ạ
Có bài mẫu là câu a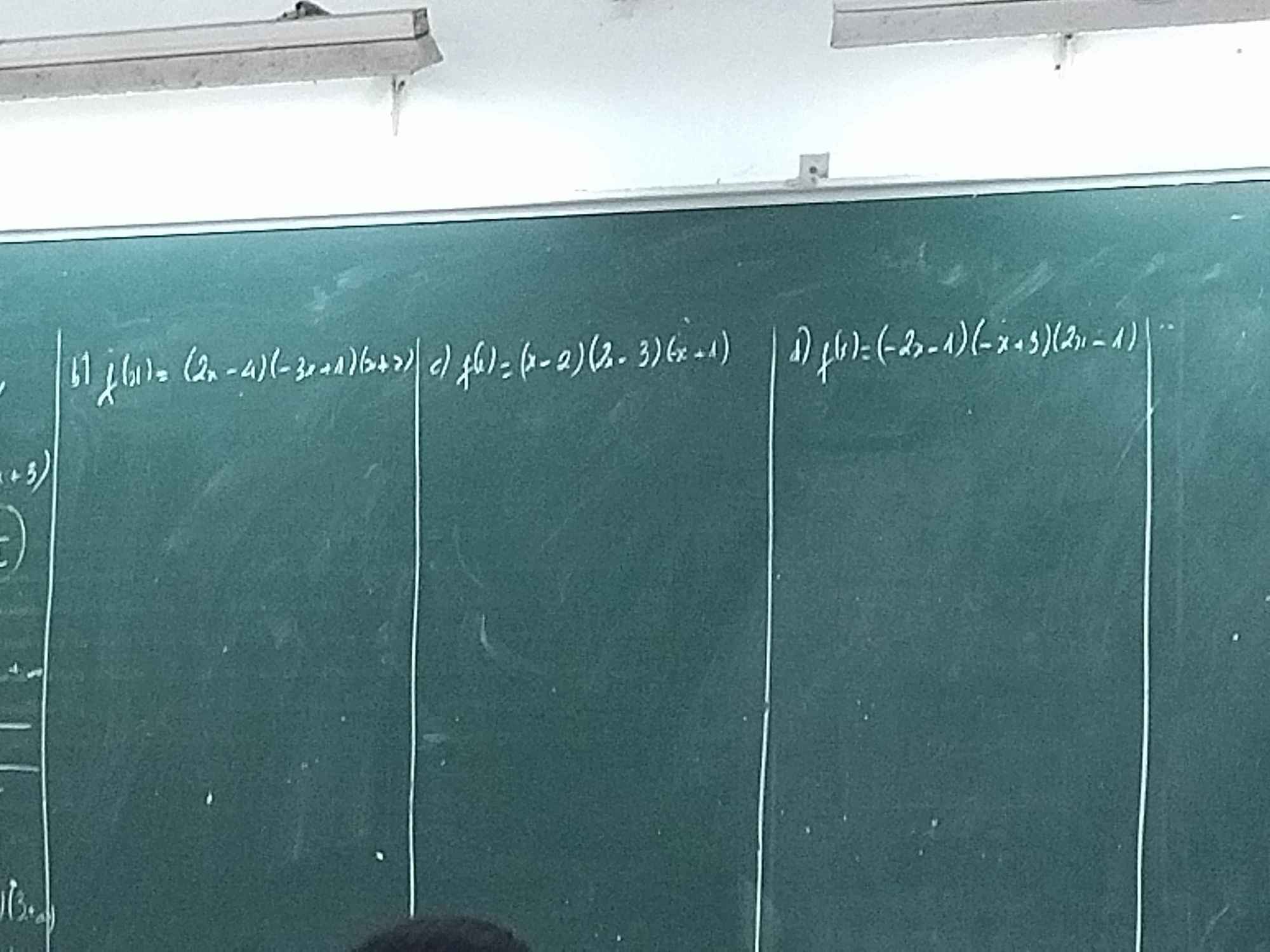
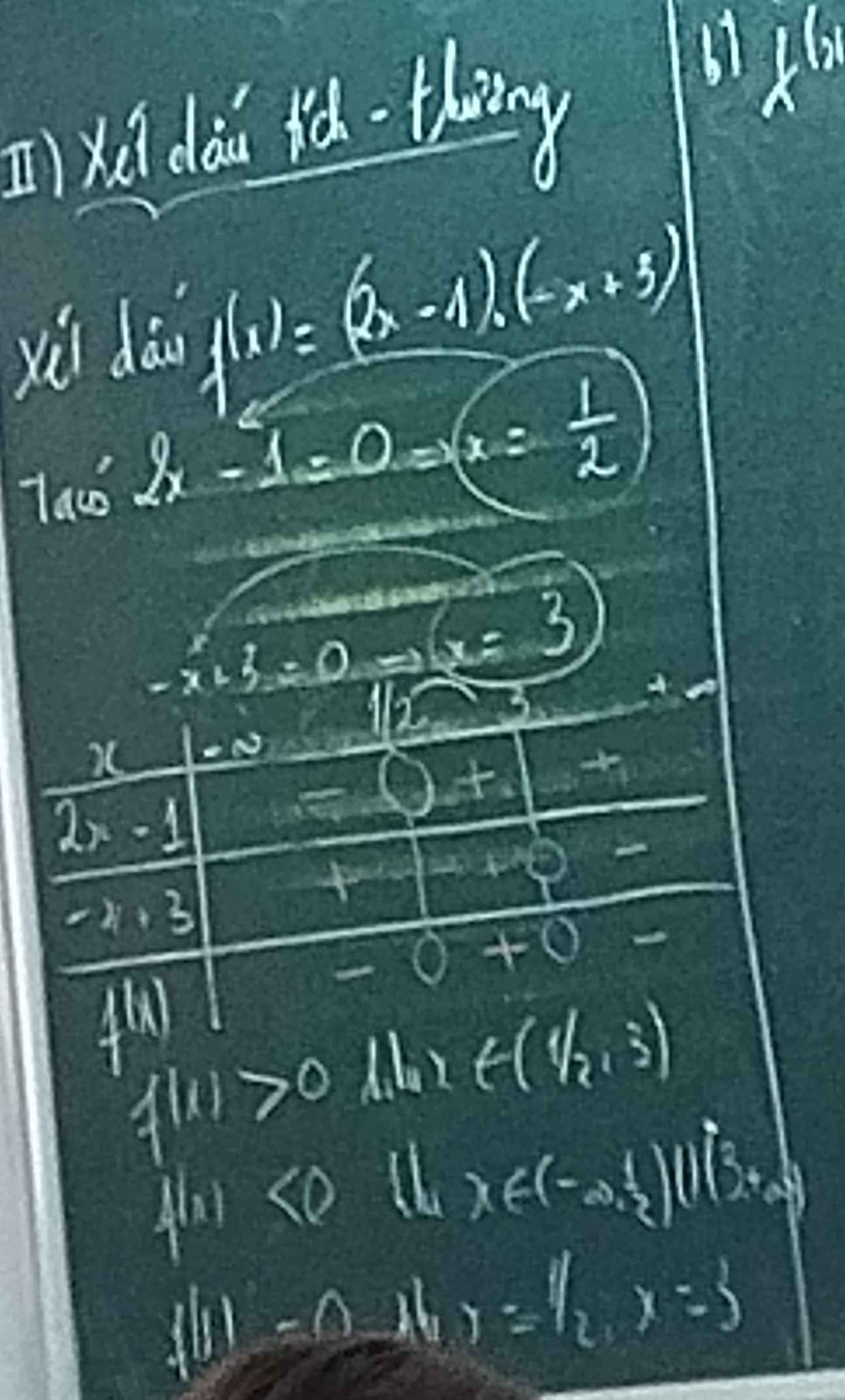

giúp em câu a) b) với ạ em cảm ơn nhìu
a: Xét (O) có
\(\hat{MAB}\) là góc nội tiếp chắn cung MB
\(\hat{MAC}\) là góc nội tiếp chắn cung MC
\(\hat{MAB}=\hat{MAC}\)
Do đó: sđ cung MB=sđ cung MC
=>MB=MC
=>M nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OM là đường trung trực của BC
=>OM⊥BC
Xét (O) có
\(\hat{MCB}\) là góc nội tiếp chắn cung MB
\(\hat{MAC}\) là góc nội tiếp chắn cung MC
sđ cung MB=sđ cung MC
Do đó: \(\hat{MCB}=\hat{MAC}\)
Xét ΔMCD và ΔMAC có
\(\hat{MCD}=\hat{MAC}\)
góc CMD chung
Do đó: ΔMCD~ΔMAC
=>\(\frac{MC}{MA}=\frac{MD}{MC}\)
=>\(MC^2=MD\cdot MA\)
Đúng 0
Bình luận (0)
Ai giúp em câu a, b với ạ
tbbttb - ngắt nhịp 2
bbbtbbtb - nhịp 4
Bbttbb - nhịp 2
Tbbtbbtb - nhịp 4
Đúng 0
Bình luận (0)