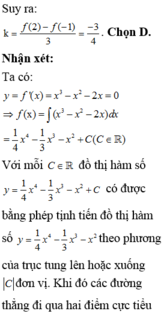Xác định hệ số góc f(x)=-3x+2,y=4x+17

Những câu hỏi liên quan
tính hệ số góc của các đường thẳng sau
f(x)=-3x+2:y=4x+17;f(x)=\(\dfrac{17}{18}x-\dfrac{7}{8}\)
Lời giải:
Hệ số góc của đường thẳng \(y=ax+b\) chính bằng $a$
Vậy:
Hsg của đường thẳng \(y=-3x+2\) là $-3$
Hsg của đường thẳng \(y=4x+17\) là $4$
Hsg của đường thẳng \(y=\frac{17}{18}x-\frac{7}{8}\) là \(\frac{17}{18}\)
Đúng 0
Bình luận (0)
Cho hàm số bậc hai y f(x) {x^2} - 4x + 3a) Xác định hệ số a. Tính f(0);f(1);f(2);f(3);f(4) và nhận xét về dấu của chúng so với dấu của hệ số ab) Cho đồ thị hàm số yf(x) (H.6.17). Xét từng khoảng left( { - infty ;1} right);left( {1;3} right);left( {3; + infty } right), đồ thị nằm phía trên hay phía dưới trục Ox?c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Đọc tiếp
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
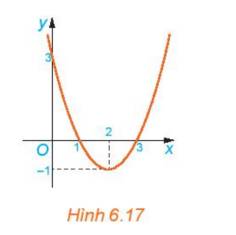
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
Đúng 0
Bình luận (0)
Cho hệ số y =f(x) xác định với mọi x thuộc R biết f(x)+5f(4) =3x2
Tính f(-3)
Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số \(a,b\) của chúng.
a) \(y = 4x + 2\); b) \(y = 5 - 3x\); c) \(y = 2 + {x^2}\);
d) \(y = - 0,2x\); e) \(y = \sqrt 5 x - 1\).
a) Hàm số \(y = 4x + 2\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = 4;b = 2\).
b) Hàm số \(y = 5 - 3x = - 3x + 5\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 3;b = 5\).
c) Hàm số \(y = 2 + {x^2}\) không phải là hàm số bậc nhất vì không có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\).
d) Hàm số \(y = - 0,2x\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 0,2;b = 0\).
e) Hàm số \(y = \sqrt 5 x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = \sqrt 5 ;b = - 1\).
Đúng 0
Bình luận (0)
a) \(y=4x+2\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)
b) \(y=5-3x\Rightarrow\left\{{}\begin{matrix}a=-2\\b=5\end{matrix}\right.\)
c) \(y=2+x^2\) không phải hàm số bậc nhất.
d) \(y=0,2x\Rightarrow\left\{{}\begin{matrix}a=-0,2\\b=0\end{matrix}\right.\)
e) \(y=\sqrt[]{5}x-1\Rightarrow\left\{{}\begin{matrix}a=\sqrt[]{5}\\b=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm tổng giá trị không thuộc tập xác định của hàm số: f(x)=3x-2/4x^3+3x-7
3x+7=28
3x =28-7
3x =21
x =21:3
x =7
Đúng 0
Bình luận (0)
Bài 6. Cho hai đa thức: f(x) 9 - x5 + 4x - 2x3 + x2 - 7x4 g(x) x5 - 9 + 2x2 +7x4 + 2x3 - 3x. a) Sắp xếp các đa thức theo luỹ thừa giảm của biến. Xác định bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức. b) Tính tổng h(x) f(x) + g(x) c) Tìm nghiệm của đa thức h(x).
Đọc tiếp
Bài 6. Cho hai đa thức: f(x) = 9 - x5 + 4x - 2x3 + x2 - 7x4
g(x) = x5 - 9 + 2x2 +7x4 + 2x3 - 3x.
a) Sắp xếp các đa thức theo luỹ thừa giảm của biến. Xác định bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
b) Tính tổng h(x) = f(x) + g(x) c) Tìm nghiệm của đa thức h(x).
a: f(x)=-x^5-7x^4-2x^3+x^2+4x+9
g(x)=x^5+7x^4+2x^3+2x^2-3x-9
b: H(x)=-x^5-7x^4-2x^3+x^2+4x+9+x^5+7x^4+2x^3+2x^2-3x-9
=3x^2+x
c: H(x)=0
=>x(3x+1)=0
=>x=0 hoặc x=-1/3
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm xác định và liên tục trên Rvới
y
f
(
x
)
x
3
-
x
2
-
2
x
. Gọi k là hệ số góc của đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số yf(x). Khẳng định nào sau đây đúng ?
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm xác định và liên tục trên Rvới y = f ' ( x ) = x 3 - x 2 - 2 x . Gọi k là hệ số góc của đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số y=f(x). Khẳng định nào sau đây đúng ?
![]()
![]()

1.Tập xác định của hàm số y= ( x2-1)2/3 là
2.hệ số góc của tiếp tuyến tại A (1;0) của đồ thị hàm số y = -x3+3x -1
3.tìm tập xác định của hàm số y= log2021(x-1)
4.bất pt 2x-1<5 có tập nghiệm là
Mong mn chỉ giúp ♡
cho (d) y = -m x + 2m - 3
và (d1) y = 3x - m + 2
tìm m, biết a. (d) // (d1)
b. (d) ⊥ (d1)
c. xác định hệ số góc và tung độ góc của (d)
a, để (d) // (d1) thì \(\left\{{}\begin{matrix}-m=3\\2m-3\ne-m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-3\\m\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow m=-3\)
b, để (d) ⊥ (d1) thì \(-m.3=-1\Rightarrow-m=-\dfrac{1}{3}\Rightarrow m=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)