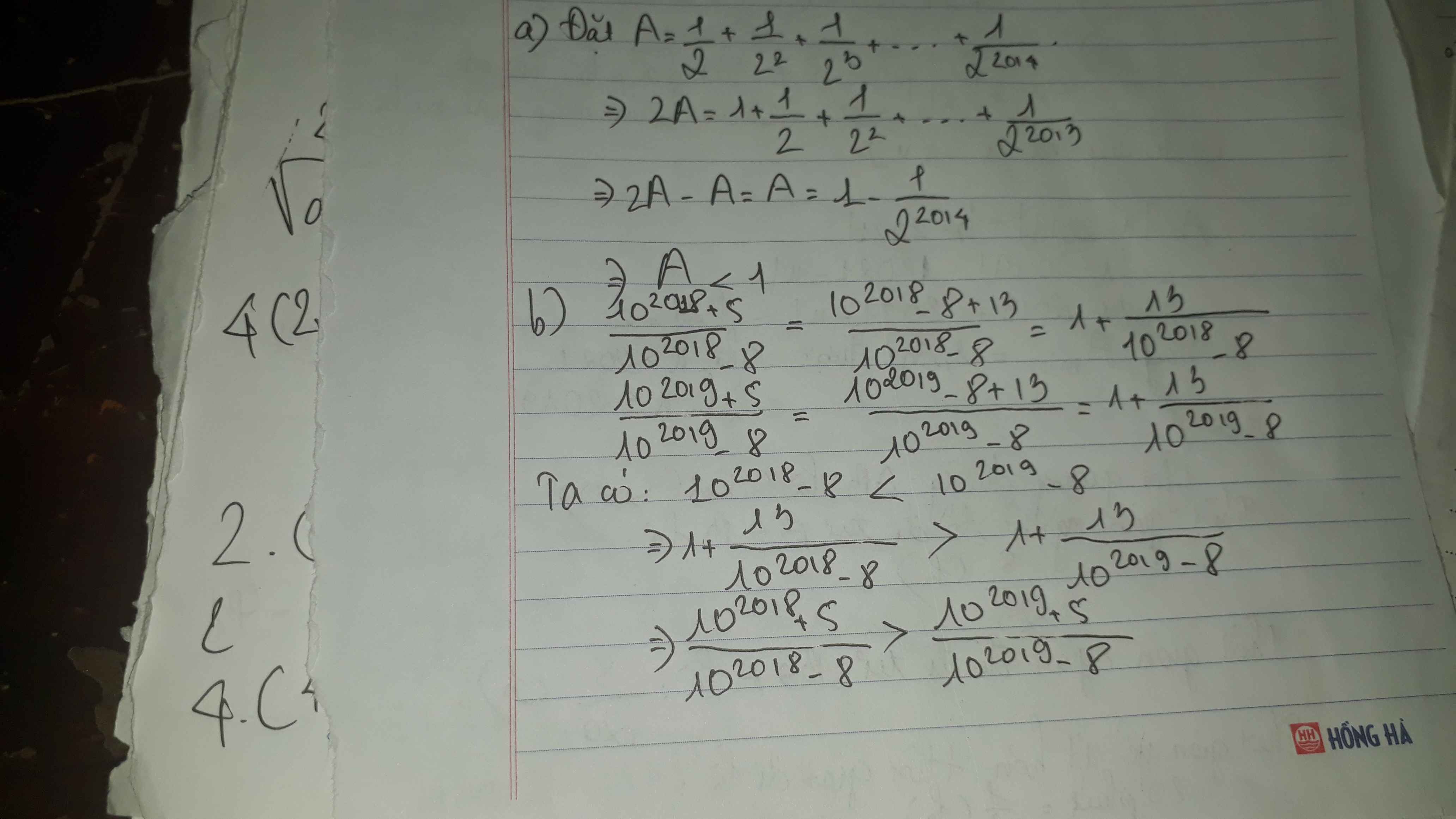So sánh \(\dfrac{1}{2!}\)+ \(\dfrac{1}{3!}\)+.......+\(\dfrac{1}{2019!}\) với \(\dfrac{1}{2}\)
Những câu hỏi liên quan
so sánh A và B biết:
A=\(\dfrac{2^{2018}}{2^{2018}+3^{2019}}\)+\(\dfrac{3^{2019}}{3^{2019}+5^{2020}}\)+\(\dfrac{5^{2020}}{5^{2020}+2^{2018}}\)
B=\(\dfrac{1}{1.2}\)+\(\dfrac{1}{3.4}\)+\(\dfrac{1}{5.6}\)+...+\(\dfrac{1}{2019.2020}\).
\(A>\dfrac{2^{2018}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{3^{2019}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{5^{2020}}{5^{2020}+2^{2018}+3^{2019}}=1\)
\(B< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2019\cdot2020}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)
=>B<1
=>A>B
Đúng 1
Bình luận (0)
1. So sánh
a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\) và B= \(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{13}{60}\)
b) \(C=\dfrac{2019}{2021}+\dfrac{2021}{2022}\) và \(D=\dfrac{2020+2022}{2019+2021}.\dfrac{3}{2}\)
a) Ta có:
2A=2.(12+122+123+...+122020+122021)2�=2.12+122+123+...+122 020+122 021
2A=1+12+122+123+...+122019+1220202�=1+12+122+123+...+122 019+122 020
Suy ra: 2A−A=(1+12+122+123+...+122019+122020)2�−�=1+12+122+123+...+122 019+122 020
−(12+122+123+...+122020+122021)−12+122+123+...+122 020+122 021
Do đó A=1−122021<1�=1−122021<1.
Lại có B=13+14+15+1360=20+15+12+1360=6060=1�=13+14+15+1360=20+15+12+1360=6060=1.
Vậy A < B.
Đúng 2
Bình luận (0)
13 tháng 3 2021 lúc 21:45
Cho tổng \(T=\dfrac{2}{2^1}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{2020}{2^{2019}}+\dfrac{2021}{2^{2020}}\)
So sánh T với 3
\(2T=2+\dfrac{3}{2^1}+\dfrac{4}{2^2}+...+\dfrac{2020}{2^{2018}}+\dfrac{2021}{2^{2019}}\)
\(T=2T-T=2+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2019}}-\dfrac{2021}{2^{2020}}\).
Đặt \(S=\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2019}}\Rightarrow2S=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2018}}\Rightarrow S=2S-S=1-\dfrac{1}{2^{2019}}\).
Từ đó \(T=2+1-\dfrac{1}{2^{2019}}-\dfrac{2021}{2^{2020}}< 3\).
Đúng 4
Bình luận (0)
16 tháng 7 2021 lúc 13:27
Bài 6: So sánha,dfrac{1}{2}+dfrac{1}{_{ }2^2}+dfrac{1}{2_{ }^3}+...+dfrac{1}{2^{2014}}và 1 b,dfrac{10^{2018}+5}{10^{2018}-8}và dfrac{10^{2019}+5}{10^{2019}-8}c,dfrac{1}{1.2.3}+dfrac{1}{2.3.4}+dfrac{1}{3.4.5}+...+dfrac{1}{23.24.25}vàdfrac{1}{4}
Đọc tiếp
Bài 6: So sánh
a,\(\dfrac{1}{2}\)+\(\dfrac{1}{_{ }2^2}\)+\(\dfrac{1}{2_{ }^3}\)+...+\(\dfrac{1}{2^{2014}}\)và 1 b,\(\dfrac{10^{2018}+5}{10^{2018}-8}\)và \(\dfrac{10^{2019}+5}{10^{2019}-8}\)
c,\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{23.24.25}\)và\(\dfrac{1}{4}\)
22 tháng 3 2023 lúc 11:30
\(S=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\) so sánh S với \(\dfrac{1}{2}\)
\(3S=1+\dfrac{1}{3}+...+\dfrac{1}{3^{99}}\)
=>2S=1-1/3^100
=>S=1/2-1/2*3^100<1/2
Đúng 0
Bình luận (0)
So sánh \(A\) với \(\dfrac{3}{4}\), biết \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
1/32< 1/2.3
1/42< 1/3.4
...
1/1002< 1/99.100
=> 1/22 + 1/32 + 1/42 + ... + 1/1002< 1/22 + 1/2.3 + 1/3.4 + ... + 1/99.100
A < 1/4 + 1/2 -1/3 + 1/3 - 1/4 +... + 1/99 - 1/100
A < 1/4 + 1/2 -1/100 < 1/4 + 1/2 = 3/4
=> A < 3/4
Đúng 1
Bình luận (0)
Cho M = \(1-\dfrac{1}{2}-\dfrac{1}{2^2}-\dfrac{1}{2^3}-\dfrac{1}{2^4}-....-\dfrac{1}{2^{10}}\) . So sánh M với \(\dfrac{1}{2^{11}}\)
\(M=1-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}\right)\)
Đặt \(N=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}\)
\(2N=1+\dfrac{1}{2}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2N-N=1-\dfrac{1}{2^{10}}\)
\(\Rightarrow N=1-\dfrac{1}{2^{10}}\)
\(\Rightarrow M=1-\left(1-\dfrac{1}{2^{10}}\right)=\dfrac{1}{2^{10}}>\dfrac{1}{2^{11}}\)
Vậy \(M>\dfrac{1}{2^{11}}\)
Đúng 2
Bình luận (1)
12 tháng 5 2021 lúc 20:40
So sánh : \(A=\dfrac{2019^{2020}+1}{2019^{2019}-1}\) và \(B=\dfrac{2019^{2019}+1}{2019^{2018}-1}\)
Lời giải:
Ta có:
\(A+1=\frac{2019^{2019}+2019^{2020}}{2019^{2019}-1}=\frac{2019^{2019}.2020}{2019^{2019}-1}\)
\(B+1=\frac{2019^{2019}+2019^{2018}}{2019^{2018}-1}=\frac{2019^{2018}.2020}{2019^{2018}-1}\) \(=\frac{2019^{2019}.2020}{2019^{2019}-2019}>\frac{2019^{2019}.2020}{2019^{2019}-1}\)
$\Rightarrow B+1>A+1$
$\Rightarrow B>A$
Đúng 2
Bình luận (0)
so sánh: \(A=\dfrac{9^{2019}+1}{9^{2020}+1}\) và \(B=\dfrac{9^{2018}+1}{9^{2019}+1}\)
giúp mình với mn.
Lời giải:
\(9B=\frac{9^{2019}+9}{9^{2019}+1}=1+\frac{8}{9^{2019}+1}> 1+\frac{8}{9^{2020}+1}=\frac{9^{2020}+9}{9^{2020}+1}=9A\)
$\Rightarrow B>A$
Đúng 0
Bình luận (0)
So sánh \(\dfrac{1}{11}\)+ \(\dfrac{1}{12}\) +...+ \(\dfrac{1}{19}\)+ \(\dfrac{1}{20}\) với \(\dfrac{2}{3}\)