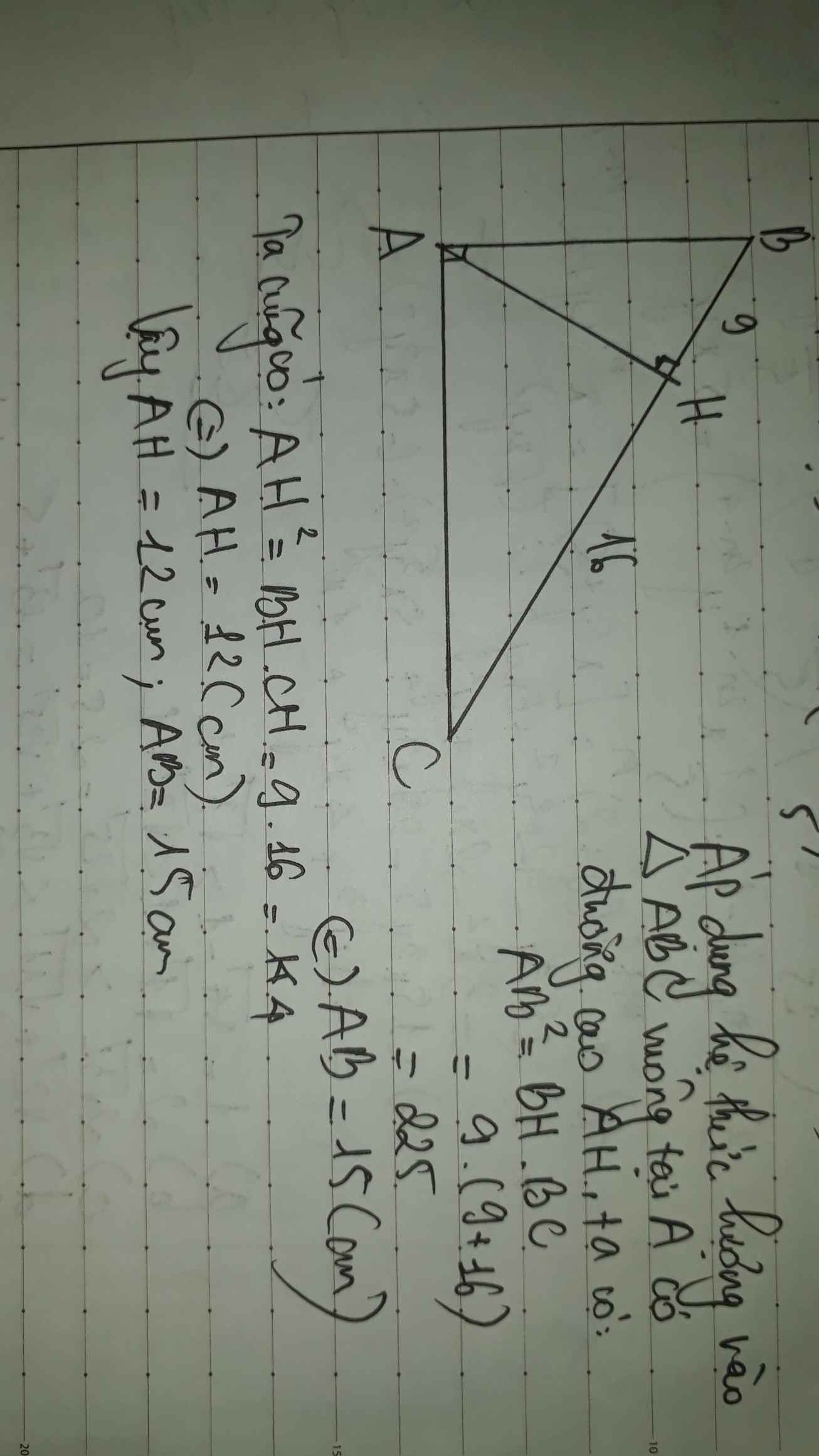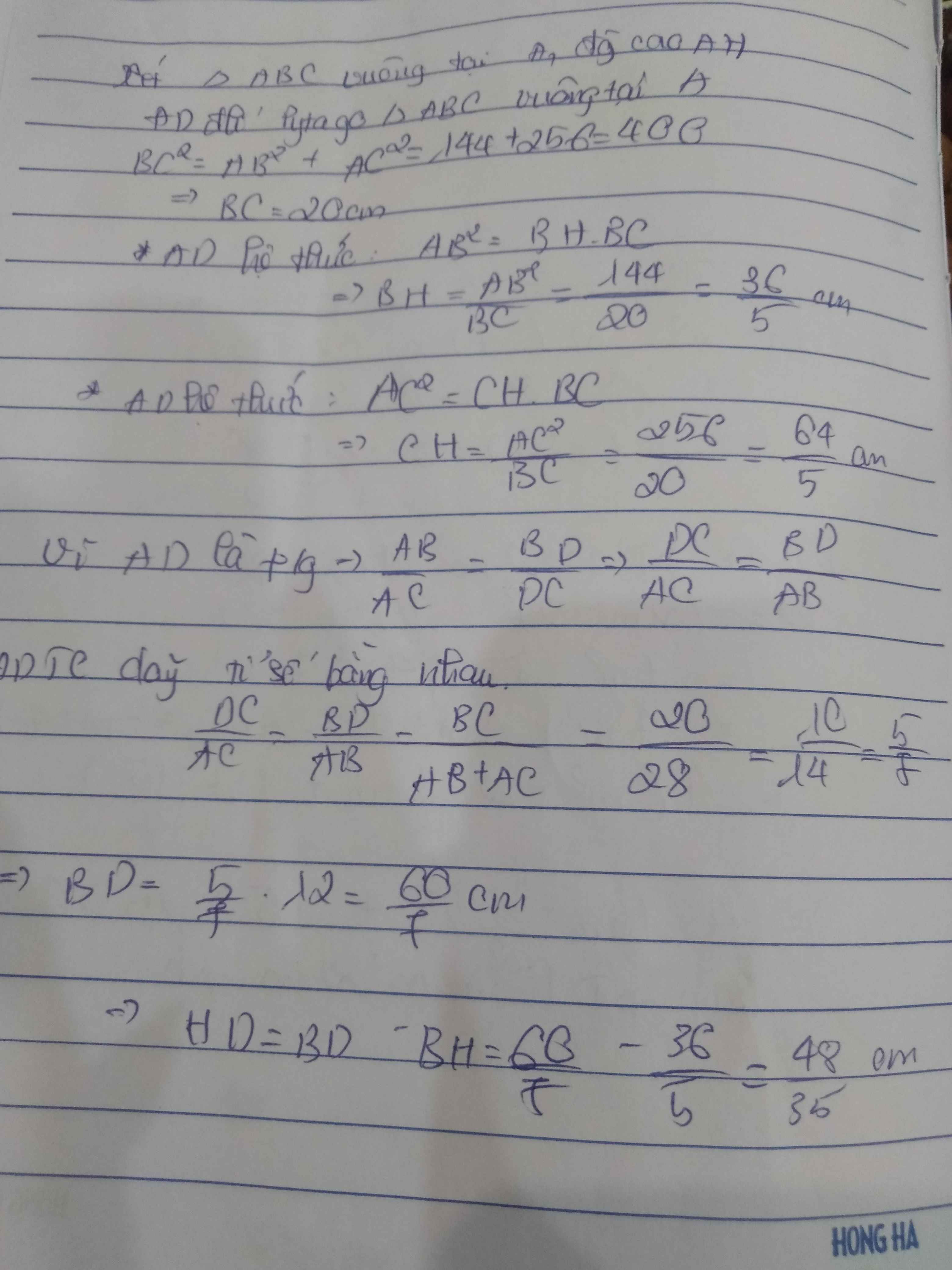\(a,BC=HB+HC=25\left(cm\right)\)

Áp dụng HTL:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=225\\AC^2=CH\cdot BC=400\\AH^2=BH\cdot CH=144\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Vì \(\widehat{ADH}=\widehat{AEH}=\widehat{BAC}=90^0\) nên ADHE là hcn

Do đó \(DE=AH=12\left(cm\right)\)

a) + AH2 = BH.CH = 9.16 = 144 AH = 12cm

+ AB2 = BH. BC = 9.25 AB  = 15cm

+ AC2 =  CH.BC = 16.25 AC = 20cm  

b) Chứng minh được tứ giác ADHE là hình chữ nhật  

c) +HD.AB = HA.HB HD = HA.HB/AB= 12.9/15 = 7,2cm

+HE.AC = HA.HC HE = HA.HC /AC = 12.16/20 = 9,6cm

+ Chu vi ADHE:  (HD + HE ).2 = (7,2 + 9,6).2 = 33,6(cm)  

 + SADHE = HD.HE = 7,2. 9,6  =  69,12(cm2)  

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:

AH²=BH.HC=9.16=144

<=>AH=√144=12((cm)

Áp dụng định lý Pytago vào tam giác vuông BHA ta có:

BA²=AH²+BH²=12²+9²=225

<=>BA=√225=15(cm)

Áp dụng định lý Pytago vào tam giác vuông CHA ta có:

CA²=AH²+CH²=12²+16²=20(cm)

Vậy AB=15cm,AC=20cm,AH=12cm

Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
(HC tự tính nha)

a: Xét ΔABC vuông tại A có AH là đường cao

nên AB^2=BH*BC

b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)

\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)

=>AC=20(cm)

1) 

a) Xét ΔABC có 

\(BC^2=AC^2+AB^2\left(7.5^2=4.5^2+6^2\right)\)

nên ΔABC vuông tại A(Định lí Pytago đảo)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:

\(AB\cdot AC=AH\cdot BC\)

\(\Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{4.5\cdot6}{7.5}=\dfrac{27}{7.5}=3.6\left(cm\right)\)

Vậy: AH=3,6cm

b) Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:

\(AC^2=AH^2+CH^2\)

\(\Leftrightarrow CH^2=4.5^2-3.6^2=7.29\)

hay CH=2,7(cm)

Ta có: BH+CH=BC(H nằm giữa B và C)

nên BH=BC-CH=7,5-2,7=4,8(cm)

Vậy: BH=4,8cm; CH=2,7cm

1.a)Ta có:7,5²=4,5²+6² nên theo định lí Py-ta-go 

=>\(\Delta ABC\) vuông tại A

Ta có: AB.AC=BC.AH

=> \(AH=\dfrac{AC.AB}{BC}=\dfrac{4,5.6}{7,5}=3.6\)  (cm)

b)Ta có:AB²=BC.BH

  \(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{7,5}=4,8\) (cm)

Ta có:BH+CH=BC

     =>CH=BC-BH=7,5-4,8=2,7 (cm)

AC^2=HC*CB

=>HC(HC+7,2)=16^2=256

=>HC^2+7,2*HC-256=0

=>HC=12,8cm

AH=căn 12,8*7,2=9,6cm

BC=12,8+7,2=20cm

AB=căn 7,2*20=12(cm)

AC=căn 12,8*20=16(cm)