Tìm đk của biến để các biểu thức sau có nghĩa
a. \(\dfrac{5x}{4x^2-9}+\sqrt{\dfrac{13}{5-x}}\)
Tìm đk để các biểu thức sau có nghĩa:
1. \(\sqrt{3x^{2}-x+2}\)
2. \((\dfrac{1}{\sqrt{x}-1}+\dfrac{2}{2-\sqrt{x}}): \dfrac{x}{\sqrt{2x+1}}\)
1: ĐKXĐ: 3x^2-x+2>=0
=>x thuộc R
2: ĐKXĐ: x>=0 và căn x-1<>0 và 2-căn x<>0 và 2x+1>0 và x<>0
=>x>0 và x<>1 và x<>4
Cho biểu thức: \(A\) = \(\left(\dfrac{3+\sqrt{x}}{3-\sqrt{x}}-\dfrac{3-\sqrt{x}}{3+\sqrt{x}}-\dfrac{4x}{x-9}\right)\) : \(\left(\dfrac{5}{3-\sqrt{x}}-\dfrac{4\sqrt{x}+2}{3\sqrt{x}-x}\right)\) . Tìm đk của x để |A| > - A
ĐKXĐ: x>0; x<>9
\(A=\left(\dfrac{-\left(\sqrt{x}+3\right)}{\sqrt{x}-3}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{4x}{x-9}\right):\left(\dfrac{5\sqrt{x}-4\sqrt{x}-2}{\sqrt{x}\left(3-\sqrt{x}\right)}\right)\)
\(=\dfrac{-x-6\sqrt{x}-9+x-6\sqrt{x}+9-4x}{x-9}:\dfrac{-\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-4x-12\sqrt{x}}{x-9}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{-\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4x\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(x-9\right)\left(\sqrt{x}-2\right)}=\dfrac{4x}{\sqrt{x}-2}\)
|A|>-A
=>A>=0
=>4x>0
=>x>0 và x<>9
Tìm đk để các biểu thức sau có nghĩa:
a) \(\sqrt{\dfrac{-1}{10-5x}}\)
b) \(\dfrac{7}{\sqrt{7-3x}}\)
c) \(\sqrt{-5-2x}\)
a) ĐKXĐ: \(10-5x< 0\Leftrightarrow5x>10\Leftrightarrow x>2\)
b) ĐKXĐ: \(7-3x>0\Leftrightarrow3x< 7\Leftrightarrow x< \dfrac{7}{3}\)
c) ĐKXĐ: \(-5-2x\ge0\Leftrightarrow2x\le-5\Leftrightarrow x\le-\dfrac{5}{2}\)
a) \(x>2\)
b) \(x< \dfrac{7}{3}\)
c) \(x\le-\dfrac{5}{2}\)
a: ĐKXĐ: x>2
b: ĐKXĐ: \(x< \dfrac{7}{3}\)
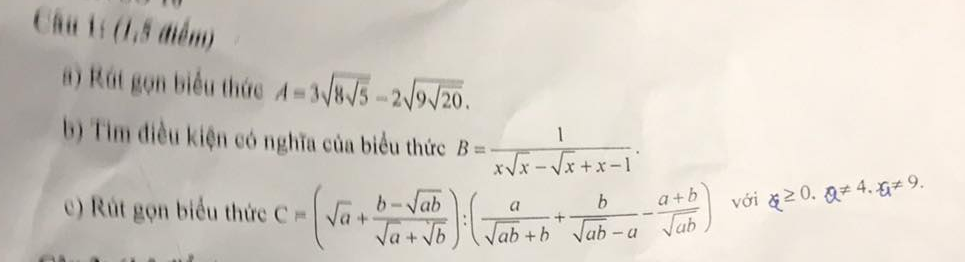
c1
a. rút gọn biểu thức
\(A=3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\)
b. tìm đk có nghĩa của biểu thức
\(B=\dfrac{1}{x\sqrt{x}-\sqrt{x}+x-1}\)
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
1) Tính giá trị của biểu thức : A= 3\(\sqrt{\dfrac{1}{3}}\) - \(\dfrac{5}{2}\)\(\sqrt{12}\) - \(\sqrt{48}\)
2) Tìm x để biểu thức sau có nghĩa : A=\(\sqrt{12-4x}\)
3) Rút gọn biểu thức : P= \(\dfrac{2x-2\sqrt{x}}{x-1}\) với x≥0 và x ≠1
1) \(A=3\sqrt{\dfrac{1}{3}}-\dfrac{5}{2}\sqrt{12}-\sqrt{48}\)
\(=3\cdot\dfrac{\sqrt{1}}{\sqrt{3}}-\dfrac{5\sqrt{12}}{2}-\sqrt{4^2\cdot3}\)
\(=\dfrac{3\cdot1}{\sqrt{3}}-\dfrac{5\cdot2\sqrt{3}}{2}-4\sqrt{3}\)
\(=\sqrt{3}-5\sqrt{3}-4\sqrt{3}\)
\(=-8\sqrt{3}\)
2) \(A=\sqrt{12-4x}\) có nghĩa khi:
\(12-4x\ge0\)
\(\Leftrightarrow4x\le12\)
\(\Leftrightarrow x\le\dfrac{12}{4}\)
\(\Leftrightarrow x\le3\)
3) \(\dfrac{2x-2\sqrt{x}}{x-1}\)
\(=\dfrac{2\sqrt{x}\cdot\sqrt{x}-2\sqrt{x}}{\left(\sqrt{x}\right)^2-1^2}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{\text{x}}}{\sqrt{x}+1}\)
tìm x để biểu thức sau có nghĩa
a) \(\dfrac{1}{\sqrt{4x^2-12x+9}}\)
b) \(\dfrac{1}{\sqrt{x^2-x+1}}\)
giải chi tiết hộ mình với ạ !!!
a: ĐKXĐ: \(x\ne\dfrac{3}{2}\)
b: ĐKXĐ: \(x\in R\)
Tìm x để mỗi căn thức sau có nghĩa:
a. \(\sqrt{3-2x}\) b. \(\sqrt{x+1}+\sqrt{3-x}\) c. \(\dfrac{\sqrt{4x-2}}{x^2-4x+3}\) d. \(\dfrac{\sqrt{4x^2-2x+1}}{\sqrt{3-5x}}\)
ĐKXĐ: \(3-2x\ge0\Leftrightarrow x\le\dfrac{3}{2}\)
b) ĐKXĐ: \(-1\le x\le3\)
c) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ne1\\x\ne3\end{matrix}\right.\).
d) ĐKXĐ: \(x< \dfrac{3}{5}\).
\(\sqrt{2x+11}+\sqrt{x-1}\) ; \(\dfrac{\sqrt{-5x}}{x}\) ; \(\dfrac{\sqrt{7x^2+1}}{5}\); \(\sqrt{x^2-14x+33}\); \(\dfrac{\sqrt{-x^2+6x+16}}{-2}+\dfrac{x^2-2x}{3x^2}\)
Tìm ĐKXĐ của x để các biểu thức trên có nghĩa
a: ĐKXĐ: \(x\ge1\)
b: ĐKXĐ: \(x< 0\)
c: ĐKXĐ: \(\left[{}\begin{matrix}x\ge11\\x\le3\end{matrix}\right.\)
1) ĐKXĐ: \(\left\{{}\begin{matrix}2x+11\ge0\\x-1\ge0\end{matrix}\right.\)\(\Leftrightarrow x\ge1\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}-5x\ge0\\x\ne0\end{matrix}\right.\)\(\Leftrightarrow x< 0\)
3) ĐKXĐ: \(7x^2+1\ge0\left(đúng\forall x\right)\Leftrightarrow x\in R\)
4) ĐKXĐ: \(x^2-14x+33\ge0\Leftrightarrow\left(x-11\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-11\ge0\\x-3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-11\le0\\x-3\le0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge11\\x\le3\end{matrix}\right.\)
5) ĐKXĐ:
+) \(-x^2+6x+16\ge0\)
\(\Leftrightarrow-\left(x^2-6x+9\right)+25\ge0\)
\(\Leftrightarrow\left(x-3\right)^2\le25\Leftrightarrow-5\le x-3\le5\)
\(\Leftrightarrow-2\le x\le8\)
+) \(3x^2\ne0\Leftrightarrow x\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}-2\le x\le8\\x\ne0\end{matrix}\right.\)
tìm x để các biểu thức sau có nghĩa:
a)\(\sqrt{\left(x-2\right)}\)+\(\dfrac{1}{x-5}\) b)\(\sqrt{\left(2x-6\right)\left(7-x\right)}\) c)\(\sqrt{4x^2-25}\)
d)\(\dfrac{2}{x^2-9}\)-\(\sqrt{5-2x}\) e)\(\dfrac{x}{x^2-4}\)+\(\sqrt{x-2}\)
a) \(\sqrt{x-2}+\dfrac{1}{x-5}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
b) \(\sqrt{\left(2x-6\right)\left(7-x\right)}=\sqrt{2\left(x-3\right)\left(7-x\right)}\) có nghĩa khi:
\(\left(x-3\right)\left(7-x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-3\ge0\\7-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-3\le0\\7-x\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge3\\x\le7\end{matrix}\right.\\\left\{{}\begin{matrix}x\le3\\x\ge7\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3\le x\le7\)
c) \(\sqrt{4x^2-25}=\sqrt{\left(2x-5\right)\left(2x+5\right)}\) có nghĩa khi:
\(\left(2x-5\right)\left(2x+5\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x-5\ge0\\2x+5\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}2x-5\le0\\2x+5\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{5}{2}\\x\ge-\dfrac{5}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{5}{2}\\x\le-\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{5}{2}\\x\le-\dfrac{5}{2}\end{matrix}\right.\)
d) \(\dfrac{2}{x^2-9}-\sqrt{5-2x}=\dfrac{2}{\left(x+3\right)\left(x-3\right)}-\sqrt{5-2x}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\\5-2x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm3\\x\le\dfrac{5}{2}\end{matrix}\right.\)
e) \(\dfrac{x}{x^2-4}+\sqrt{x-2}=\dfrac{x}{\left(x+2\right)\left(x-2\right)}+\sqrt{x-2}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\\x-2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm2\\x\ge2\end{matrix}\right.\)
\(\Leftrightarrow x>2\)