-5x^2 +20x - 49 =A
tìm min , max
Tìm min,max của A=-|-5x-12|.|3x+2|-5x+1
phan duy em mời giải giải ko dc tau cho ăn phân
Tìm min và max của: \(A=\sqrt{5x-x^2}+\sqrt{18+3x-x^2}\)
\(dkxđ\Leftrightarrow\left\{{}\begin{matrix}-x^2+5x\ge0\\-x^2+3x+18\ge0\end{matrix}\right.\)\(\Rightarrow0\le x\le5\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\le5\end{matrix}\right.\)
\(\Rightarrow A=\sqrt{5x-x^2}+\sqrt{18+3x-x^2}\)
\(\sqrt{5x-x^2}=\sqrt{-\left(x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}\right)}=\sqrt{-\left[\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\right]}=\sqrt{-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}}\ge0\left(1\right)\)
\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=5\)
\(\sqrt{-x^2+3x+18}=\sqrt{-\left(x^2-3x-18\right)}=\sqrt{-\left[x^2-3x+\dfrac{9}{4}-\dfrac{81}{4}\right]}=\sqrt{-\left(x-\dfrac{3}{2}\right)^2+\dfrac{81}{4}}\ge\sqrt{-\left(5-\dfrac{3}{2}\right)^2+\dfrac{81}{4}}=\sqrt{8}\left(2\right)\)
dấu"=" xảy ra \(< =>x=5\)
\(\left(1\right)\left(2\right)\Rightarrow A\ge\sqrt{8}\) \(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=5\)\(\Rightarrow MinA=\sqrt{8}\)
\(\left(maxA=\sqrt{48}\right)dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=\dfrac{15}{7}\)
\(\)
1)TÌM H min = \(\sqrt{x^2+4}+\sqrt{x^2+8x+17}\)
2) tìm G min,max A=3x+x\(\sqrt{5-x^2}\)
3)tìm min,max B=\(\sqrt{5x-x^2}+\sqrt{18+3x-x^2}\)
câu 1
ta có .....
lười viết Min - cốp xki nha
DKXD của A, ta có \(x^{2\le5\Rightarrow-\sqrt{5}\le x\le\sqrt{5}}\)
mà \(3x\ge-3\sqrt{5}\)
mặt kkhác \(\sqrt{5-x^2}\ge0\Rightarrow A=3x+x\sqrt{5-x^2}\ge-3\sqrt{5}\)
min A= \(-3\sqrt{5}\)\(\Leftrightarrow x=-\sqrt{5}\)
ta có \(A^2\le25\)và ta cx có \(-5\le A\le5\)
nhưng dễ thấy \(A=-5\)không xảy ra, vô lí nên ...........bạn xem đoạn sau nhé ( tiếp phần kia )
Tìm giá trị min, max nếu có thể.
A=|5x+2|+5|x+1|
a, Ta có (x+2)2≥0(x+2)2≥0
⇒(x+2)2+5≥5⇒(x+2)2+5≥5
⇒30(x+2)2+5≤305=6⇒30(x+2)2+5≤305=6
Hay A≤6A≤6
Dấu = xảy ra ⇔(x+2)2=0⇔x+2=0⇔x=−2⇔(x+2)2=0⇔x+2=0⇔x=−2
b,
Ta có (x−3)2≥0(x−3)2≥0
⇒(x−3)2+4≥4⇒(x−3)2+4≥4
⇒20(x+2)2+5≤204=5⇒20(x+2)2+5≤204=5
Hay A≤5A≤5
Dấu = xảy ra ⇔(x−3)2=0⇔x−3=0⇔x=3⇔(x−3)2=0⇔x−3=0⇔x=3
c,
Ta có (x+1)2≥0(x+1)2≥0
⇒(x+1)2+2≥2⇒(x+1)2+2≥2
⇒10(x+1)2+2≤102=5⇒10(x+1)2+2≤102=5
Hay A≤5A≤5
Dấu = xảy ra ⇔(x+1)2=0⇔x+1=0⇔x=−1⇔(x+1)2=0⇔x+1=0⇔x=−1
A = | 5x + 2 | + 5| x + 1 |
= | 5x + 2 | + | 5x + 5 |
= | 5x + 2 | + | -( 5x + 5 ) |
= | 5x + 2 | + | -5x - 5 |
Áp dụng bất đẳng thức | a | + | b | ≥ | a + b | ta có :
A = | 5x + 2 | + | -5x - 5 | ≥ | 5x + 2 - 5x - 5 | = | -3 | = 3
Dấu "=" xảy ra khi ab ≥ 0
=> ( 5x + 2 )( -5x - 5 ) ≥ 0
1. \(\hept{\begin{cases}5x+2\ge0\\-5x-5\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}5x\ge-2\\-5x\ge5\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge-\frac{2}{5}\\x\le-1\end{cases}}\)( loại )
2. \(\hept{\begin{cases}5x+2\le0\\-5x-5\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}5x\le-2\\-5x\le5\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le-\frac{2}{5}\\x\ge-1\end{cases}}\Leftrightarrow-1\le x\le-\frac{2}{5}\)
=> MinA = 3 <=> \(-1\le x\le-\frac{2}{5}\)
Cho: \(20x^2+11y^2=2008\)
Tìm Min, Max: \(N=2\sqrt{5}x+\sqrt{11}y\)
\(N^2\le2\left(20x^2+11y^2\right)=4016\)\(\Leftrightarrow\)\(-4\sqrt{251}\le N\le4\sqrt{251}\)
\(\hept{\begin{cases}N_{min}=-4\sqrt{251}\left(x=-\sqrt{\frac{251}{5}};y=-\sqrt{\frac{1004}{11}}\right)\\N_{max}=4\sqrt{251}\left(x=\sqrt{\frac{251}{5}};y=\sqrt{\frac{1004}{11}}\right)\end{cases}}\)
Tìm min, max
5x-2x2+1
Cấy ni chỉ tìm được Max thôi
5x - 2x2 + 1
= -2( x2 - 5/2x + 25/16 ) + 33/8
= -2( x - 5/4 )2 + 33/8 ≤ 33/8 ∀ x
Dấu "=" xảy ra khi x = 5/4
Vậy GTLN của biểu thức = 33/8 <=> x = 5/4
5x - 2x2 + 1
= - 2x2 + 5x -\(\frac{25}{8}+\frac{33}{8}\)
= - 2 ( x -\(\frac{5}{4}\))2 +\(\frac{33}{8}\le\frac{33}{8}\)
Dấu "=" xảy ra <=> - 2 ( x - 5/4 )2 = 0 <=> x - 5/4 = 0 <=> x = 5/4
Vậy maxB = 33/8 <=> x = 5/4
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
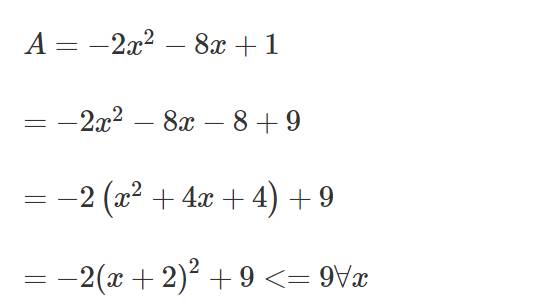
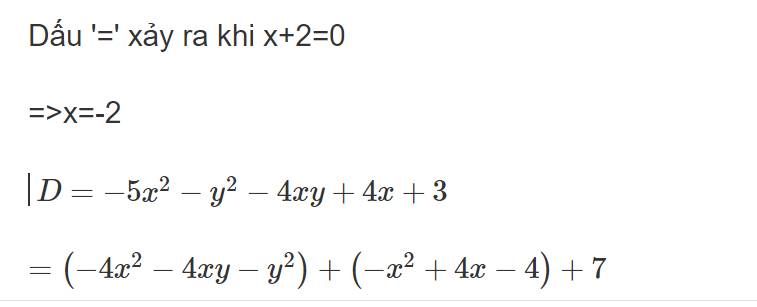
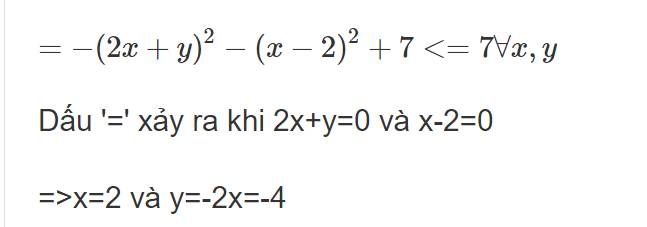
có bài nào làm theo hàng đẳng thức thì làm giùm vs
a , tìm max
A = 4x-x^2+3
B =x-x^2
b tìm Min
Q = x^2-20x= 101
M= x^2 - 4xy + 5y^2 + 10x -22y +28
a, +/ Có \(A=4x-x^2+3=4x-x^2+4-1\)
\(=-\left(-2.2x+x^2+2^2\right)+1=1-\left(x-2\right)^2\)
do \(\left(x-2\right)^2\ge0\forall x\in R\Rightarrow A\le1\)
\(\Rightarrow maxA=1\)tại \(\left(x-2\right)^2=0\Rightarrow x-2=0\Rightarrow x=2\)
Vậy max A=1 tại x=2
+/ Có \(B=x-x^2=2.\frac{1}{2}x-x^2-\frac{1}{4}+\frac{1}{4}\)
\(=-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}\right)+\frac{1}{4}=\frac{1}{4}-\left(x-\frac{1}{2}\right)^2\)
\(\Rightarrow A\le\frac{1}{4}\)do\(\left(x-\frac{1}{2}\right)^2\ge0\forall x\Rightarrow maxB=\frac{1}{4}\)tại \(\left(x-\frac{1}{2}\right)^2=0\Rightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)
Vậy max B =\(\frac{1}{4}\)tại x=\(\frac{1}{2}\)
Tìm Min Max của \(C=\frac{x^2}{x^2-5x+7}\)
\(C=\frac{x^2}{x^2-5x+7}\)
\(\Leftrightarrow Cx^2-5Cx+7C=x^2\)
\(\Leftrightarrow\left(C-1\right)x^2-5Cx+7C=0\)
Để phương trình có nghiệm thì
\(\Delta=25C^2-4.7C.\left(C-1\right)=-3C^2+28C\ge0\)
\(\Leftrightarrow0\le C\le\frac{28}{3}\)
Vậy GTNN là 0 và GTLN là \(\frac{28}{3}\)
\(C=\frac{x^2}{x^2-5x+7}=\frac{1}{\frac{7}{x^2}-\frac{5}{x}+1}=\frac{1}{7t^2-5t+1}\) với \(t=\frac{1}{x}\) (Xét với \(x\ne0\))
Tới đây dễ dàng giải tiếp.