cho 2 khoảng A = ( m;m+1) và B=(3:5) tìm m để A \(\cup\) B là 1 khoảng.
Gt chi tiết giúp mình vs !!!
Những câu hỏi liên quan
cho khoảng A=(-∞;5-4m) và khoảng B=(2-m;∞) tìm tất cả số thực m để A\B=A
Để A \ B = A thid 5 - 4m < 2 - m
⇔-4m + m < 2 - 5
⇔ -3m < -3
⇔ m > 1
Vậy m > 1 thì A \ B = A
Đúng 0
Bình luận (0)
Cho 2 khoảng A= (m ; m+1) và B=(3 ; 5). Tìm m để AUB là một khoảng.
Câu 14: cho khoảng A = ( -∞ ; 6 / 2-m ) và khoảng B=(1-m ; + ∞ ) tìm tất cả các số thực để A \ B = A
ĐKXĐ: m<>2
Để A\B=A thì A giao B=rỗng
Để \(A\cap B=\varnothing\) thì \(\dfrac{6}{2-m}< =1-m\)
=>\(\dfrac{6-\left(1-m\right)\left(2-m\right)}{2-m}< =0\)
=>\(\dfrac{6-\left(m-2\right)\left(m-1\right)}{m-2}>=0\)
=>\(\dfrac{6-m^2+3m-2}{m-2}>=0\)
=>\(\dfrac{-m^2+3m+4}{m-2}>=0\)
=>\(\dfrac{m^2-3m-4}{m-2}< =0\)
=>\(\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}< =0\)
Đặt \(F\left(x\right)=\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}\)
Đặt m-4=0
=>m=4
Đặt m+1=0
=>m=-1
Đặt m-2=0
=>m=2
Ta có bảng xét dấu:
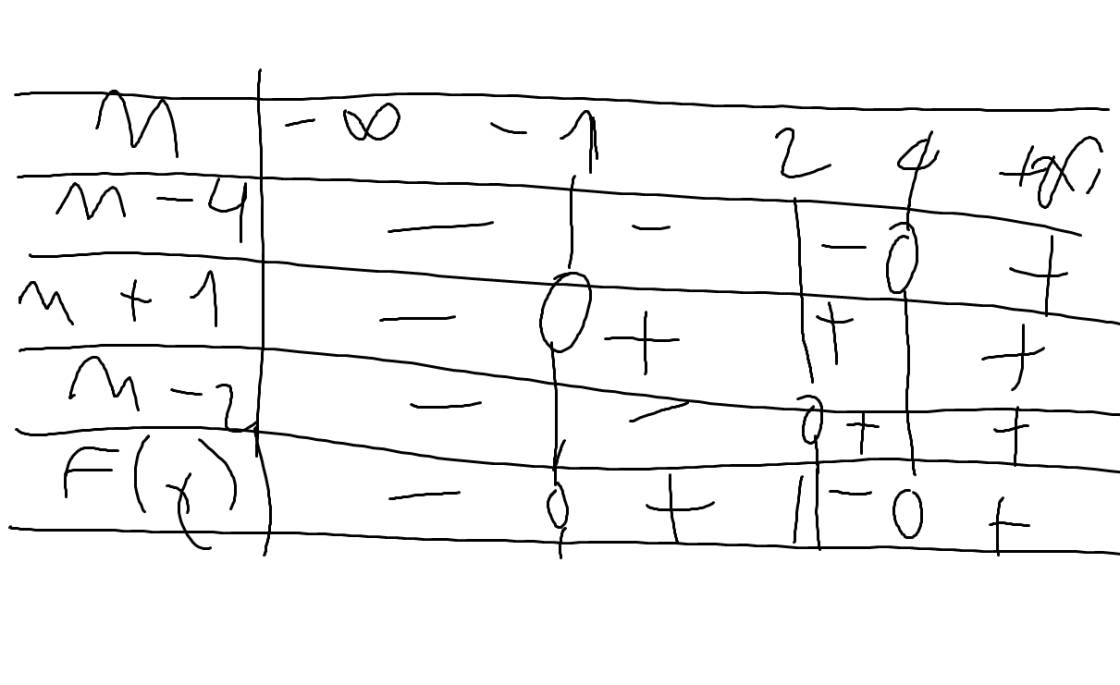
Theo BXD, ta có:F(x)<=0
=>\(\left[{}\begin{matrix}m< =-1\\2< m< =4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mp Oxy, cho A(1;3), B(-2:2)
tìm trên đường thẳng ab điểm M sao cho khoảng cách từ M đến Ox bằng khoảng cách từ M đến Oy
Gọi e thuộc ab 2 tiếp tuyến của C qua E lần lượt là H,K biết HK=2
Đúng 0
Bình luận (0)
Tìm m sao cho:
a, \(A\cup B=R\) biết \(A=(-\infty;3];B=[m;+\infty)\)
b, \(C\cup D\) là một khoảng (tùy theo m xác định khoảng đó), biết \(C=\left(m;m+2\right);D=\left(-3;1\right)\)
Cho 2 tập hợp :
A= (m , m+1)
B= ( 2 , 5)
Tìm điều kiện m để :
a/ \(A\cap B\)
b/ \(A\cup B\) là một khoảng , tìm khoảng đó
Cho 2 tập hợp :
A= (m , m+1)
B= ( 2 , 5)
Tìm điều kiện m để :
a/ A \(\cap\) B
b/ A \(\cup\) B là một khoảng , tìm khoảng đó
a) Cho A(2 ; 4) và B(5 ; 2). Tìm trên trục hoành điểm M sao cho tổng khoảng cách từ M tới A và B là nhỏ nhất.
b) Cho A(–6 ; –2) và B (–3 ; –4). Tìm trên trục hoành điểm M sao cho tổng khoảng cách từ M tới A và B là nhỏ nhất.
Cho đường thẳng d: y=x-5
a) Tìm các điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng d bằng 2.
b) Tìm các điểm N thuộc trục Oy sao cho khoảng cách từ N đến đường thẳng d bằng 2.