giúp mình nhé

1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)

Vậy hpt có nghiệm (x;y) = (3;4)

2)

a) 3x² - 2x - 1 = 0

\(\Leftrightarrow3x^2-3x+x-1=0\)

\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)

Vậy pt có nghiệm x = 1 hoặc x = 3

b) Đặt x² = t (t \(\ge\) 0)

Pt trở thành: t² - 20t + 4 = 0

\(\Delta\) = (-20)² - 4.1.4 = 400 - 16 = 384

=> pt có 2 nghiệm phân biệt t₁ = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)

t₂ = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)

=> x₁ = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)

x₂ = \(2-\sqrt{6}\)

\(a,\left\{{}\begin{matrix}x+y=3\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+2y=6\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5y=5\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=1\\2x-3.1=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Vậy \(\left(x;y\right)=\left(2;1\right)\)

b, \(x^2-7x+10=0\\ \Leftrightarrow x^2-5x-2x+10=0\\ \Leftrightarrow x\left(x-5\right)-2\left(x-5\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

\(a,\)\(\left\{{}\begin{matrix}x+y=3\\2x-3y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x+3y=9\\2x-3y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-3y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2.2-3y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(2;1\right)\)

\(b,x^2-7x+10=0\)

\(\Delta=b^2-4ac=\left(-7\right)^2-4.10=9>0\)

\(\Rightarrow\) Pt có 2 nghiệm \(x_1,x_2\)

Ta có :

\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{7+3}{2}=5\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{7-3}{2}=2\end{matrix}\right.\)

Vậy \(S=\left\{5;2\right\}\)

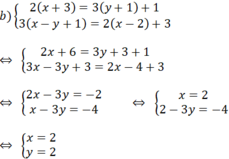
Vậy hệ phương trình đã cho có nghiệm (x; y) =(2; 2).

\(\left\{{}\begin{matrix}5x-4y=32\\2x+3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}10x-8y=64\\10x+15y=-5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-23y=69\\2x+3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=4\end{matrix}\right.\)

Vậy hpt có nghiệm là \(\left(x;y\right)=\left(4;-3\right)\)

\(\left\{{}\begin{matrix}5x-4y=32\\2x+3y=-1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}5x-4y=32\\5x+7,5y=-\dfrac{5}{2}\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}5x-4y=32\\-\dfrac{23}{2}y=\dfrac{69}{2}\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=4\\y=-3\end{matrix}\right.\)

Vậy HPT có nghiệm (x;y) = (4;-3)

\(\left\{{}\begin{matrix}5x-4y=32\\2x+3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x-8y=64\\10x+15y=-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-1\\-23y=69\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3.\left(-3\right)=-1\\y=-3\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=4\\y=-3\end{matrix}\right.\)

Bạn xem lại đề, ở pt thứ nhất là \(3x-2y+5x=14\) hay \(3x-2y+5z=14\)

Đề bị lỗi công thức rồi em nhé!

.

1: =>x^2+3x-4=0

=>(x+4)(x-1)=0

=>x=1 hoặc x=-4

2: =>2x-3y=1 và 3x=4y+2

=>2x-3y=1 và 3x-4y=2

=>x=2 và y=1