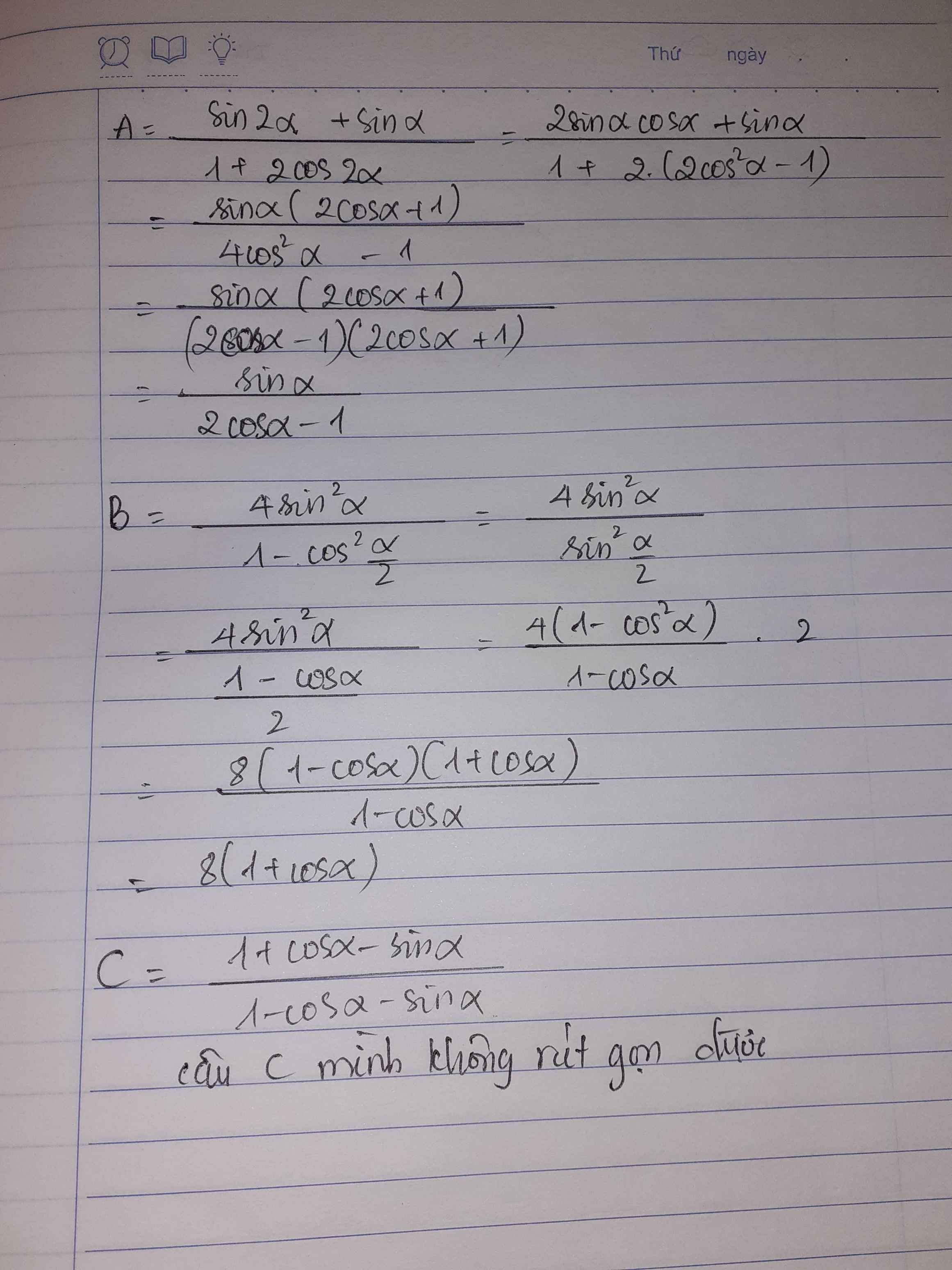a) Biết sin2=\(\dfrac{9}{15}tính\cos2,\tan2,\cot,biết\cos2=\dfrac{3}{5}tính\sin2,\tan2,\cot2\)

Những câu hỏi liên quan
Tính:
A = 5 . sin2 151π/6 + 3 . cos2 . 85π/3 - 4 tan2 . 193π/6 + 7 cot2 37π/3.
Cho sin2=0.6
Tính cos2, tan2, cotang2 (2 là anfa)
\(sin^2\alpha+cos^2\alpha=1\Rightarrow cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{1-\left(0,6\right)^2}=\frac{4}{5}\)
\(tan\alpha=\frac{sin\alpha}{cos\alpha}=\frac{0,6}{\frac{4}{5}}=\frac{3}{4}\)
\(cot\alpha=\frac{1}{tan\alpha}=\frac{1}{\frac{3}{4}}=\frac{4}{3}\)
Đúng 0
Bình luận (0)
chứng minh công thức nhân đôi
\(\sin2\alpha=2.\sin\alpha.\cos\alpha\)
\(\cos2\alpha=\cos^2\alpha-\sin^2\alpha\)
\(\tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha}\)
Chứng minh đẳng thức
a) \(\dfrac{1-sin2\alpha+cos2\alpha}{1+sin2\alpha+cos2\alpha}=tan\left(\dfrac{\pi}{4}-\alpha\right)\)
b) \(\dfrac{1-cos\alpha+cos2\alpha}{sin2\alpha-sin\alpha}=cot\alpha\)
\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
Đúng 0
Bình luận (0)
cho tan∂ =2 . tính Cot2 , Sin2, Cos2
\(\cot\alpha=\dfrac{1}{2}\)
\(\sin\alpha=\dfrac{kề}{\sqrt{5}kề}=\dfrac{\sqrt{5}}{5}\)
\(\cos\alpha=\sqrt{1-\dfrac{5}{25}}=\dfrac{2\sqrt{5}}{5}\)
Đúng 0
Bình luận (0)
Bài 11: Cho tam giác ABC vuông tại A có BC = a; CA = b; AB = c, đường cao AH. a. Chứng minh: 1 + tan2 B = 1 cos2 B ; tan C 2 = c a+b . b. Chứng minh: AH = a. sin B . cos B , BH = a. cos2 B , CH = a. sin2 B.
Cho \(\cos\alpha=-\dfrac{2}{3}\) và \(\dfrac{\pi}{2}< \alpha< \pi\). Biết \(K=\sin2\alpha+cos2\alpha=x+y\sqrt{5}\) với x, y thuộc Q và \(\dfrac{x}{y}=\dfrac{a}{b}\) là phân số tối giản. Tính \(a-b\)
\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=\dfrac{\sqrt{5}}{3}\)
\(K=2sina.cosa+2cos^2a-1=-\dfrac{1}{9}-\dfrac{4}{9}\sqrt{5}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{1}{4}\Rightarrow a-b=-3\)
Đúng 0
Bình luận (0)
Bài 4. a) Tính giá trị biểu thức:
A = cos2 20° + cos2 40° + cos2 50° + cos2 70°.
b) Rút gọn biểu thức:
B = sin6 a + cos6 a + 3 sin2 a. cos2 a
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
Đúng 0
Bình luận (0)
Bài 1: Rút gọn:
A= \(\dfrac{sin2\alpha+sin\alpha}{1+cos2\alpha+cos2\alpha}\)
B= \(\dfrac{4sin^2\alpha}{1-cos^2\dfrac{\alpha}{2}}\)
C= \(\dfrac{1+cos\alpha-sin\alpha}{1-cos\alpha-sin\alpha}\)