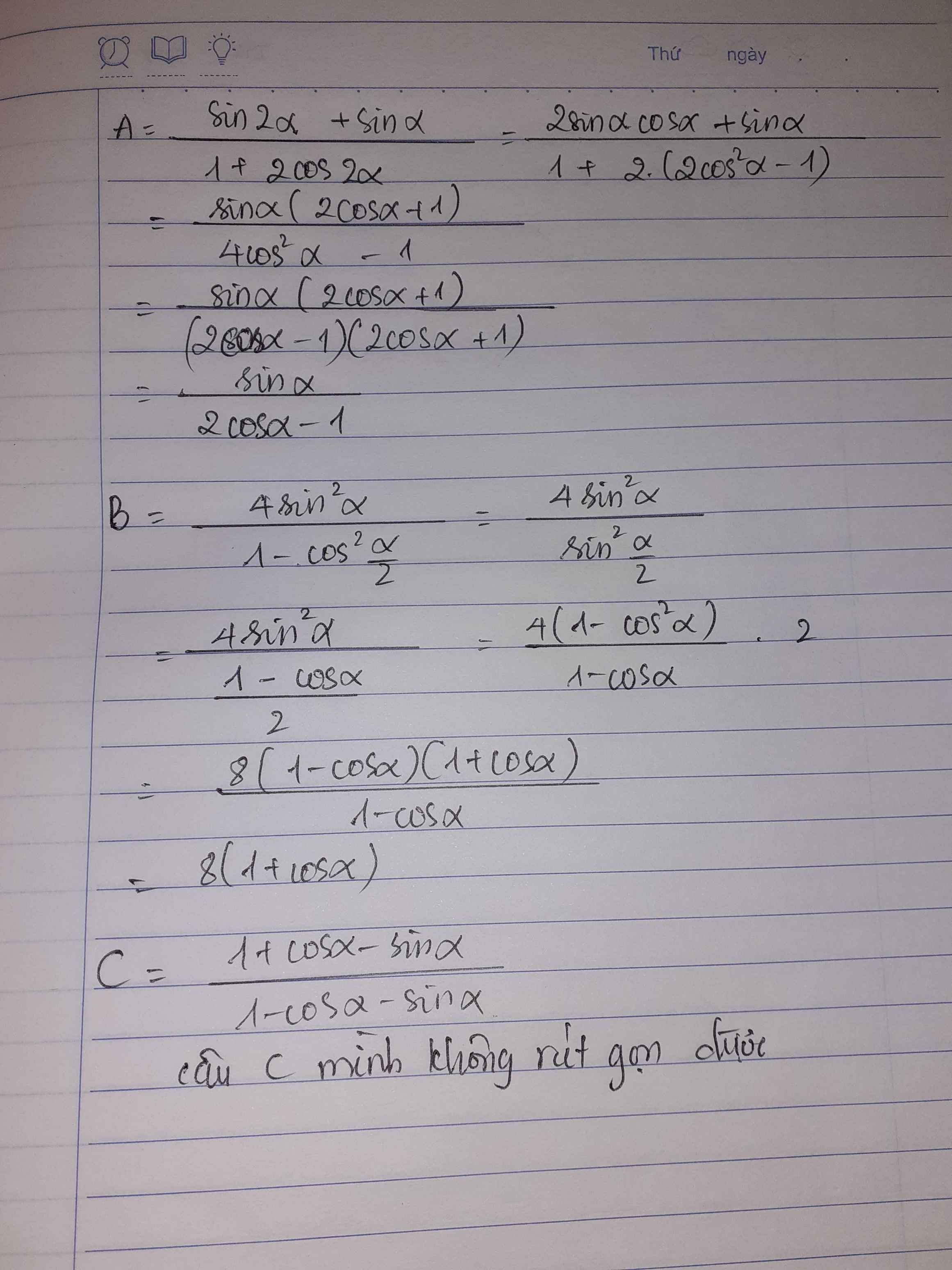Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
Các câu hỏi tương tự
Chứng minh các đẳng thức sau:
a, sin^4alpha-cos^4alpha+12sin^2alpha
b,dfrac{sin^2alpha+2cos^2alpha-1}{cot^2alpha}sin^2alpha
c, dfrac{1-sin^2alpha.cos^2alpha}{cos^2alpha}-cos^2alphatan^2alpha
d, dfrac{sin^2alpha-tan^2alpha}{cos^2alpha-cot^2alpha}tan^6alpha
e, left(1+cotalpharight)sin^3alpha+left(1+tanalpharight)cos^3alphasinalpha.cosalpha
f,dfrac{left(sinalpha+cosalpharight)^2-1}{cotalpha-sinalpha.cosalpha}2tan^2alpha
Đọc tiếp
Chứng minh các đẳng thức sau:
a, \(\sin^4\alpha-\cos^4\alpha+1=2\sin^2\alpha\)
b,\(\dfrac{\sin^2\alpha+2\cos^2\alpha-1}{\cot^2\alpha}=\sin^2\alpha\)
c, \(\dfrac{1-\sin^2\alpha.\cos^2\alpha}{\cos^2\alpha}-\cos^2\alpha=\tan^2\alpha\)
d, \(\dfrac{\sin^2\alpha-\tan^2\alpha}{\cos^2\alpha-\cot^2\alpha}=\tan^6\alpha\)
e, \(\left(1+\cot\alpha\right)\sin^3\alpha+\left(1+\tan\alpha\right)\cos^3\alpha=\sin\alpha.\cos\alpha\)
f,\(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-1}{\cot\alpha-\sin\alpha.\cos\alpha}=2\tan^2\alpha\)
Rút gọn biểu thức:
a, A = \(\dfrac{4\sin^2\alpha}{1-\cos\dfrac{\alpha}{2}}\)
b, B = \(\dfrac{1+\cos\alpha-\sin\alpha}{1-\cos\alpha-\sin\alpha}\)
c, C = \(\dfrac{1+\sin\alpha-2\sin^2\left(45^o-\dfrac{\pi}{2}\right)}{4\cos\dfrac{\alpha}{2}}\)
Tính a) sin^4α - cos^4α , biết cos2α=3/5
b) cos(α-β) biết sinα - sinβ = 1/3 và cosα - cosβ = 1/2
Rút gọn biểu thức
A= 4sin2α/1 - cos2(a/2)
B= (1 + cosα - sinα)/ (1- cosα - sinα)
a) Biến đổi sinalpha-1thành tíchb) Rút gọn biểu thức Pdfrac{cosalpha+2cos3alpha+cos5a}{sinalpha+2sin3alpha+sin5a}c) Tính giá trị biểu thức Psin30.cos60+sin60.cos30d) Giá đúng của cosdfrac{2pi}{7}+cosdfrac{4pi}{7}+cosdfrac{6pi}{7}e) Giá trị đúng của tandfrac{pi}{24}+tandfrac{7pi}{24}
Đọc tiếp
a) Biến đổi \(\sin\alpha-1\)thành tích
b) Rút gọn biểu thức \(P=\dfrac{\cos\alpha+2\cos3\alpha+\cos5a}{\sin\alpha+2\sin3\alpha+\sin5a}\)
c) Tính giá trị biểu thức \(P=\sin30.\cos60+\sin60.\cos30\)
d) Giá đúng của \(cos\dfrac{2\pi}{7}+\cos\dfrac{4\pi}{7}+\cos\dfrac{6\pi}{7}\)
e) Giá trị đúng của \(\tan\dfrac{\pi}{24}+\tan\dfrac{7\pi}{24}\)
\(F=\dfrac{\sin\alpha-2\sin\left(2\alpha\right)+\sin\left(3\alpha\right)}{\cos\alpha-3\cos\left(2\alpha\right)+\cos\left(3\alpha\right)}\)
Mn rút gọn giùm mình biểu thức này với. Mình cảm ơn ạ :<
Cho \(\alpha\) , \(\beta\in\left(0;\dfrac{\pi}{2}\right)\) và sin \(\alpha\) = \(\dfrac{1}{\sqrt{5}}\) ; Cos \(\alpha\) = \(\dfrac{1}{\sqrt{10}}\) . Tính Cos \(\left(\alpha+\beta\right)\)
Chứng minh:
\(\dfrac{1-cos\alpha-cos2\alpha+cos3\alpha}{1-2cos\alpha}=2sin^2\alpha\)
Với α là góc nhọn. CMR:
a) Cosα = 2cos^2 α - 1 = 1 - 2sin^2 α
b) sin2α = 2 . sinα . cosα