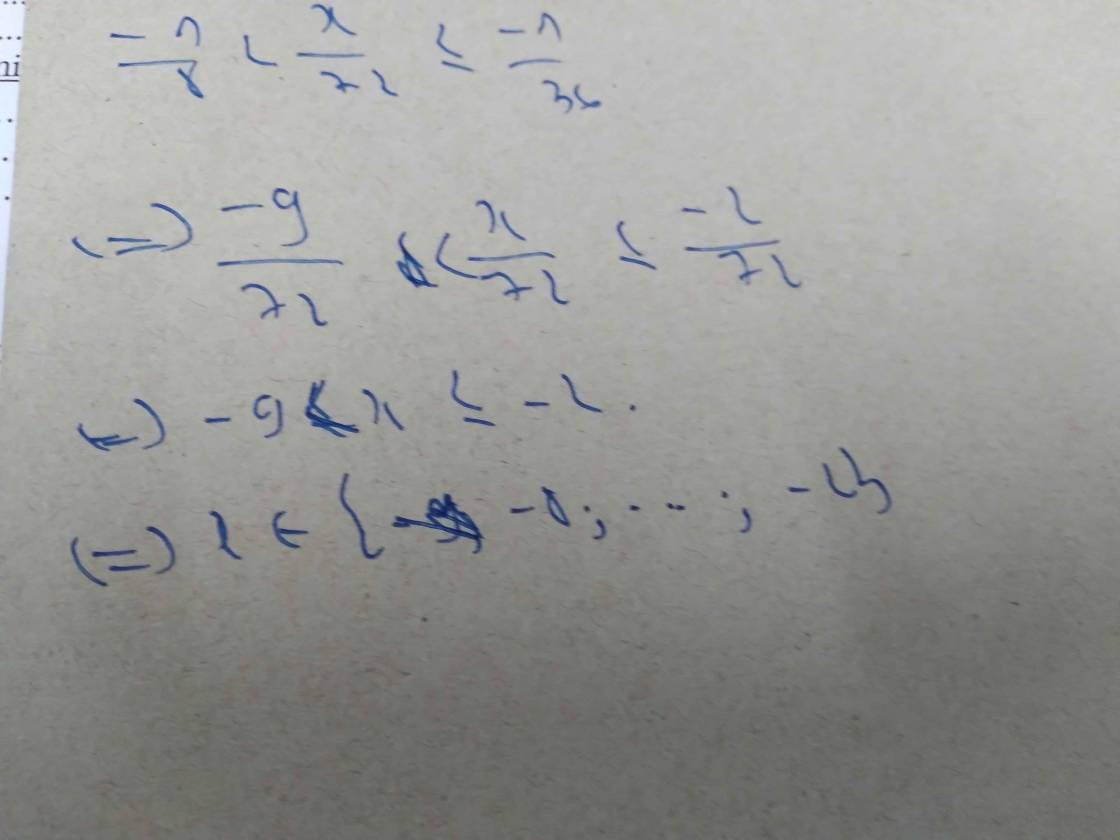Có: \(4.\frac{-3}{10}\le x\le\frac{3}{11}.\frac{11}{30}\Rightarrow\frac{-6}{5}\le x\le\frac{1}{10}\)

\(\Rightarrow-\frac{12}{10}\le x\le\frac{1}{10}\) mà x là số nguyên \(\Rightarrow x=-1\)

help me

Bn phải cho điều kiện của x nữa chứ:

VD: x là số tự nhiên hay x là số nguyên,...v.v...

\(-\dfrac{1}{8}< \dfrac{x}{72}\le-\dfrac{1}{36}\)
\(\Rightarrow\dfrac{-9}{72}< \dfrac{x}{72}\le-\dfrac{2}{72}\)
\(\Rightarrow x\in\left\{-8;-7;-6;-5;-4;-3;-2\right\}\)

`(-1)/8 < x/72 <= (-1)/36`

`(-1xx9)/(8xx9) < x/72 <=  (-1xx2)/(36xx2)`

`(-9)/72 < x/72 <=   (-2)/72`

`-> -9< x <=   (-2)`

`-> x=-8;-7;-6;-5;-4;-3;-2`

`@ yngoc`

A

Áp dụng BĐT cosi ta có 

\(\sqrt{\left(2x-1\right).1}\le\frac{2x-1+1}{2}=x\)

\(x\sqrt{5-4x^2}\le\frac{x^2+5-4x^2}{2}=\frac{-3x^2+5}{2}\)

Khi đó 

\(A\le3x+\frac{-3x^2+5}{2}=\frac{-3x^2+6x+5}{2}=\frac{-3\left(x-1\right)^2}{2}+4\le4\)

MaxA=4 khi \(\hept{\begin{cases}2x-1=1\\x^2=5-4x^2\\x=1\end{cases}\Rightarrow}x=1\)

B

Áp dụng BĐT cosi ta có :

\(x^2+y^2+z^2\ge\frac{1}{3}\left(x+y+z\right)^2\)

=> \(x+y+z\le\sqrt{3\left(x^2+y^2+z^2\right)}\)

=> \(B\le\frac{xyz.\left(\sqrt{3\left(x^2+y^2+z^2\right)}+\sqrt{x^2+y^2+z^2}\right)}{\left(x^2+y^2+z^2\right)\left(xy+yz+xz\right)}=\frac{xyz.\left(\sqrt{3}+1\right)}{\left(xy+yz+xz\right)\sqrt{x^2+y^2+z^2}}\)

Lại có \(x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}\); \(xy+yz+xz\ge3\sqrt[3]{x^2y^2z^2}\)

=> \(\sqrt{x^2+y^2+z^2}\left(xy+yz+xz\right)\ge3\sqrt[3]{x^2y^2z^2}.\sqrt{3\sqrt[3]{x^2y^2z^2}}=3\sqrt{3}.xyz\)

=> \(B\le\frac{\sqrt{3}+1}{3\sqrt{3}}=\frac{3+\sqrt{3}}{9}\)

\(MaxB=\frac{3+\sqrt{3}}{9}\)khi x=y=z

Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{  - 2; - 1;0;1;2;3\} \)

Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\}  = \{  - 2;3\} \)

Khi đó:

Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{  - 1;0;1;2\} \).

 Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)

\(\frac{2}{3}\) .\(\frac{3}{4}\)\(\le\)\(\frac{x}{18}\) \(\le\)\(\frac{7}{3}\).\(\frac{1}{3}\)

\(\frac{1}{2}\le\frac{x}{18}\le\frac{7}{9}\)

\(\frac{9}{18}\le\frac{x}{18}\le\frac{14}{18}\)

\(\Rightarrow x\in\){9:10;11;12;13;14}

\(\frac{2}{3}.\left(\frac{1}{2}+\frac{3}{4}-\frac{1}{3}\right)\le\frac{x}{18}\le\frac{7}{3}.\left(\frac{1}{2}-\frac{1}{6}\right)\)

\(\frac{2}{3}.\left(\frac{5}{4}-\frac{1}{3}\right)\le\frac{x}{18}\le\frac{7}{3}.\frac{1}{3}\)

\(\frac{2}{3}.\frac{11}{12}\le\frac{x}{18}\le\frac{7}{9}\)

\(\frac{11}{18}\le\frac{x}{18}\le\frac{7}{9}\)

\(\frac{11}{18}\le\frac{x}{18}\le\frac{14}{18}\)

Vậy \(x\in\left\{11;12;13\right\}\)

\(\frac{2}{3}\cdot\left(\frac{1}{2}+\frac{3}{4}-\frac{1}{3}\right)\le\frac{x}{18}\le\frac{7}{3}\cdot\left(\frac{1}{2}-\frac{1}{6}\right)\)

\(\frac{2}{3}\cdot\left(\frac{2}{4}+\frac{3}{4}-\frac{1}{3}\right)\le\frac{x}{18}\le\frac{7}{3}\cdot\left(\frac{3}{6}-\frac{1}{6}\right)\)

\(\frac{2}{3}\cdot\left(\frac{5}{4}-\frac{1}{3}\right)\le\frac{x}{18}\le\frac{7}{3}\cdot\frac{1}{3}\)

\(\frac{2}{3}\cdot\left(\frac{15}{12}-\frac{4}{12}\right)\le\frac{x}{18}\le\frac{7}{9}\)

\(\frac{2}{3}\cdot\frac{11}{12}\le\frac{x}{18}\le\frac{7}{9}\)

\(\frac{11}{18}\le\frac{x}{18}\le\frac{14}{18}\)

Để \(x\)phải nhỏ hơn hoặc bằng thì x lần lượt bằng \(\left\{11;12;13;14\right\}\)

\(a,\)\(A=\left\{x\in R|x< 3\right\}\Rightarrow A=\left(\text{ -∞;3}\right)\)

\(B=\left\{-1;0;1;2;3;4;5\right\}\)

\(\Rightarrow A\cap B=\left\{-1;0;1;2\right\}\)

\(b,x=-1\Rightarrow y=1-2\left(-1\right)+m=m+3\) 

\(x=1\Rightarrow y=1-2+m=m-1\)

\(\Rightarrow C=(m-1;m+3]\subset A\)

\(\Rightarrow C\subset A\Leftrightarrow m+3< 3\Leftrightarrow m< 0\)

a) I 2x-5 I = 13

=> 2x-5 =13 => x=9 

hoặc 2x-5= -13 => x=\(\dfrac{-8}{2}\)

a) | 2x-5 | = 13

=>2x-5 = 13   hoặc   2x-5 = -13

+)2x-5 = 13

=>2x = 13+5 =18

+)2x-5 =-13

=>2x=-13+5 = -8

=>x=-4

Vậy x thuộc {9;-4}

Vậy x=9

b)|7x+3|=66

=>7x+3 = 66     hoặc   7x+3 = -66

+)7x+3=66

=>7x=66-3=63

=>x=9

+)7x+3=-66

=>7x=-66-3=-69

=>x=-69/7  (loại vì x thuộc Z )

Vậy x=9

c) Có | 5x-2|\(\le\)0

mà |5x-2|\(\ge\)0

=>|5x-2|=0

=>5x-2=0

=>5x=2

=>x=2/5   ( loại vì x thuộc Z)

Vậy x=\(\varnothing\)

Giải:

a) \(\left|2x-5\right|=13\) 

\(\Rightarrow\left[{}\begin{matrix}2x-5=13\\2x-5=-13\end{matrix}\right.\) 

\(\Rightarrow\left[{}\begin{matrix}x=9\left(t\backslash m\right)\\x=-4\left(t\backslash m\right)\end{matrix}\right.\) 

b) \(\left|7x+3\right|=66\) 

\(\Rightarrow\left[{}\begin{matrix}7x+3=66\\7x+3=-66\end{matrix}\right.\) 

\(\Rightarrow\left[{}\begin{matrix}x=9\\x=\dfrac{-69}{7}\end{matrix}\right.\) 

Vì \(x\in Z\) nên x=9

c) \(\left|5x-2\right|\le0\) 

mà \(\left|5x-2\right|\ge0\) 

\(\Rightarrow\left|5x-2\right|=0\) 

       \(5x-2=0\) 

             \(5x=0+2\) 

             \(5x=2\) 

               \(x=2:5\) 

               \(x=\dfrac{2}{5}\) (loại)

Vậy \(x\in\) ∅