Cái đề này không rõ nhé bạn! Bạn ghi lại đề bằng fx nhé

Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem

\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)

\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)

\(\Rightarrow P=4\)

\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)

\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)

\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)

a. Ta có biến đổi:

\(A=\frac{a^3+2a^2-1}{a^3+2a^3+2a+1}\)

\(A=\frac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}\)

\(A=\frac{a^2+a-1}{a^2+a+1}\)

b. Gọi d là ước chung lớn nhất của \(a^2+a-1\)và \(a^2+a+1\)

Vì \(a^2+a-1=a\left(a+1\right)-1\)là số lẻ nên d là số lẻ

Mặt khác, \(2=\left[a^2+a+1-\left(a^2+a-1\right)\right]⋮d\)

Nên d = 1 tức là \(a^2+a+1\)và \(a^2+a-1\)nguyên tố cùng nhau.

Vậy biểu thức A là phân số tối giản.

giải mới like đáp án mik mất rùi

Biểu thức không hiển thị. Bạn xem lại đề.

Với  x ≥ 0 ,   x ≠ 1 ,   x ≠ 4 ta có:

Q = x + 27 . P x + 3 x − 2 = x + 27 x + 3 = x − 9 + 36 x + 3 = x − 3 + 36 x + 3 = − 6 + x + 3 + 36 x + 3 ≥ − 6 + 12 = 6

Câu 2:

a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)

=>\(2m\ne4\)

=>\(m\ne2\)

b: Thay m=0 vào (d1), ta được:

\(y=\left(0-1\right)x+2=-x+2\)

Thay m=0 vào (d2), ta được:

\(y=\left(3-0\right)x-2=3x-2\)

Vẽ đồ thị:

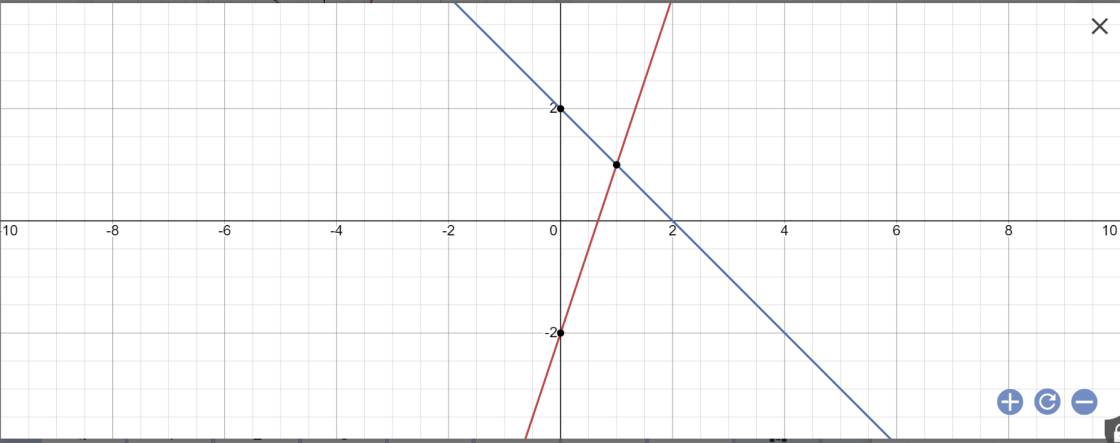
c: Phương trình hoành độ giao điểm là:

3x-2=-x+2

=>3x+x=2+2

=>4x=4

=>x=1

Thay x=1 vào y=3x-2, ta được:

y=3*1-2=3-2=1

d:

Khi m=0 thì (d2): y=3x-2

Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox

y=3x-2 nên a=3

\(tan\alpha=a=3\)

=>\(\alpha\simeq72^0\)

Câu 3:

a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H và H là trung điểm của AB

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2\)

=>\(OH\cdot OM=R^2\)

b: Ta có: AC//OM

OM\(\perp\)AB

Do đó: AB\(\perp\)AC

=>ΔABC vuông tại A

=>ΔABC nội tiếp đường tròn đường kính BC

mà ΔABC nội tiếp (O)

nên O là trung điểm của BC

=>B,O,C thẳng hàng

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE\(\perp\)EC tại E

=>BE\(\perp\)CM tại E

Xét ΔMBC vuông tại B có BE là đường cao

nên \(ME\cdot MC=MB^2\)(3)

Xét ΔMBO vuông tại B có BH là đường cao

nên \(MH\cdot MO=MB^2\left(4\right)\)

Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)

Câu 6:

Số giao điểm là:

\(\dfrac{2006\cdot2005}{2}=2011015\left(điểm\right)\)

\(1,=\left(x-y\right)^2:\left(x-y\right)^2=1\\ 2,P=\left(x+y+x-y\right)^2=4x^2\\ 3,=\left(x+1\right)^2=\left(-1+1\right)^2=0\\ 4,\)

Áp dụng PTG, độ dài đường chéo là \(\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)

Câu 1:

 \(\left(x-y\right)^2:\left(y-x\right)^2\\ =\left(x-y\right)^2:\left(x-y\right)^2\\ =1\)

Câu 2:

\(\left(x+y\right)^2+\left(x-y\right)^2+2\left(x+y\right)\left(x-y\right)=\left(x+y+x-y\right)^2=\left(2x\right)^2=4x^2\)

Câu 3:

\(x^2+2x+1=\left(x+1\right)^2=\left(-1+1\right)^2=0\)

Câu 4:

Gọi hcn đó là ABCD có chiều dài là AB, chiều rộng là AD

Áp dụng Pi-ta-go ta có:\(AB^2+AD^2=AC^2\Rightarrow AC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)

tự nhiên cho lớp 6 thành lớp 3