cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O; goác ABD =góc ACD.Gọi E là giao điểm của của hai cạnh kéo dài AD và BC.chúng minh rằng
a.tam giác AOB ~ tam giác DOC
b.tam giác AOD ~ tam giác BOC
c.EA.ED=EB.EC
`
Những câu hỏi liên quan
Cho tứ giác ABCD có AC = 10cm , BD = 12cm , hai đường chéo AC và BD cắt nhau tại O . Biết AOB = 30độ. Tính diện tích ABCD
cho tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O.Chứng minh tổng hai đường chéo AC và BD lớn hơn tổng hai cạnh đối của tứ giác
Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC, OCD và ODA.
Đúng 2
Bình luận (0)
Cho tứ giác ABCD có AC = 10cm, BD = 12cm, hai đường chéo AC và BD cắt nhau tại O. Biết góc AOB = 30°. Tính diện tích ABCD.
25 tháng 10 2023 lúc 20:16
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và góc OAD = OCB. Chứng minh tứ giác ABCD là hình bình hành.
Lưu ý: Giải cách khác ngoài cách chứng minh 2 đường chéo
Xét ΔOAD và ΔOCB có
\(\widehat{OAD}=\widehat{OCB}\)
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
Do đó: ΔOAD=ΔOCB
=>AD=BC
\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Đúng 2
Bình luận (0)
1) Cho tứ giác ABCD có AC cắt BD tại O . Biết OA = 3cm, OB = 4cm , AB =5cm , OC =2OA ; OD=2OB .
Khi đó CD bằng: A.) 5cm. B.) 10cm . C.) 15cm . D.) 20cm .
2) Cho tứ giác ABCD . Hai đường chéo AC và BD cắt nhau tại O . Gọi E là điểm trong của tam giác OCD . Số tứ giác (tứ giác lồi và tứ giác không lồi) nhận 4 trong 5 điểm A, B , .., D , E làm đỉnh là:
A) 3
B) 6
C) 9
D) 12
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O,BAO=BDC.chứng minh:
a,AB.DO=DC.AO
b,BC.DO=AD.COCO
a,
Vì tam giác BAO đồng dạng BDC
=> \(\dfrac{AB}{DC}=\dfrac{AO}{DO}\)
=> \(AB.DO=DC.AO\)
Đúng 1
Bình luận (0)
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ ABO đồng dạng △ DCO
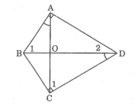
Xét △ ABO và △ DCO,ta có:
∠ (BAO) = ∠ (BDC) (gt)
Hay ∠ (BAO) = ∠ (ODC)
∠ (AOB) = ∠ (DOC) (đối đỉnh)
Vậy △ ABO đồng dạng △ DCO (g.g)
Đúng 0
Bình luận (0)
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O,
∠
(BAO)
∠
(BDC) .Chứng minh:
△
BCO đồng dạng
△
ADO
Đọc tiếp
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ BCO đồng dạng △ ADO
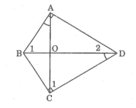
Vì △ ABO đồng dạng △ DCO nên:
∠ B 1 = ∠ C 1 (1)
Mà ∠ C 1 = ∠ C 2 = ∠ (BCD) = 90 0 (2)
Trong △ ABD, ta có: ∠ A = 90 0
Suy ra: ∠ B 1 = ∠ D 2 = 90 0 (3)
Từ (1), (2) và (3): Suy ra: ∠ C 2 = ∠ D 2
Xét △ BCO và △ ADO, ta có:
∠ C 2 = ∠ D 2 (chứng minh trên)
∠ (BOC) = ∠ (AOD) (đối đỉnh)
Vậy △ BOC đồng dạng △ ADO (g.g).
Đúng 0
Bình luận (0)
Tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết AC=4cm, BD = 5cm, A O B ^ = 60 0 . Tính diện tích tứ giác ABCD
Cho tứ giác ABCDcos AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm và đường chéo BD = 6cm.
a) Chứng minh tam giác ABD đồng dạng với tam giác BDC
b) Chứng minh tứ giác ABCD là hình thang
c) Hai đường chéo AC và BD cắt nhau tại O. Tính DO