Xét △ ABO và △ DCO,ta có:
∠ (BAO) = ∠ (BDC) (gt)
Hay ∠ (BAO) = ∠ (ODC)
∠ (AOB) = ∠ (DOC) (đối đỉnh)
Vậy △ ABO đồng dạng △ DCO (g.g)
TỨ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O, góc BOA bằng góc BDC. Chứng minh:
a) tam giác ABO đồng dạng tam giác DCO
b) tam giác BCO đồng dạng tam giác ADO
Cho tứ giác ABCD có hai góc vuông tại đỉnh A và C , hai đường chéo AC và BD cắt nhau tại O, BAO=BDC
chứng minh tam giác ABO đồng dạng với tam giác DCO
tam giác BCO đồng dạng với tam giác ADO
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ BCO đồng dạng △ ADO
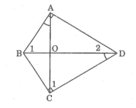
CHo tứ giác ABCD có góc A = góc C = 90, hai đường chéo AC và BD cắt nhau tại O, góc BAO = góc BDC. CM :
a. tam giác ABO đồng dạng với tam giác DCO
b. tam giác BCO đồng dạng vưới tam giác ADO
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O,BAO=BDC.chứng minh:
a,AB.DO=DC.AO
b,BC.DO=AD.COCO
Cho tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau
tại O. Biết rằng BAC=BDC . Từ O kẻ đường thẳng vuông góc với CD cắt AB tại I .
Chứng minh I là trung điểm AB
Cho tứ giác ABCD , hai dường chéo AC và BD vuông góc với nhau và cắt nhau tại điểm O . Biết \(\widehat{BAC}=\widehat{BDC}\) > từ O vẽ OK vuông góc CD tại K , đường thẳng OK cắt AB tại I . CHỨNG MINH IA = IB
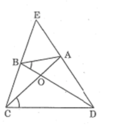
Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, ∠ (ABD) = ∠ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: △ ẠOD đồng dạng △ BOC
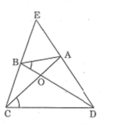
Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, ∠ (ABD) = ∠ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: △ AOB đồng dạng △ DOC
