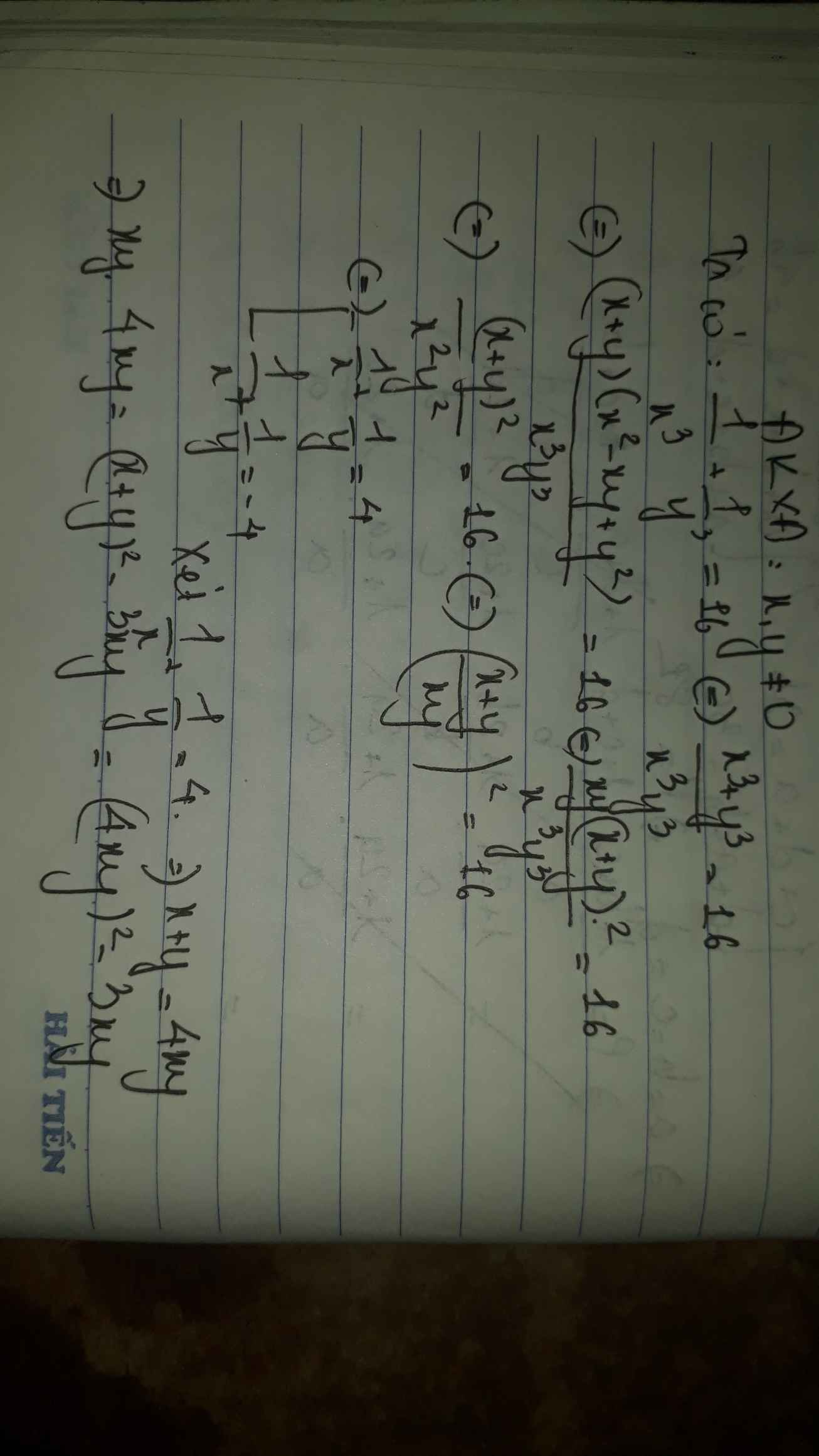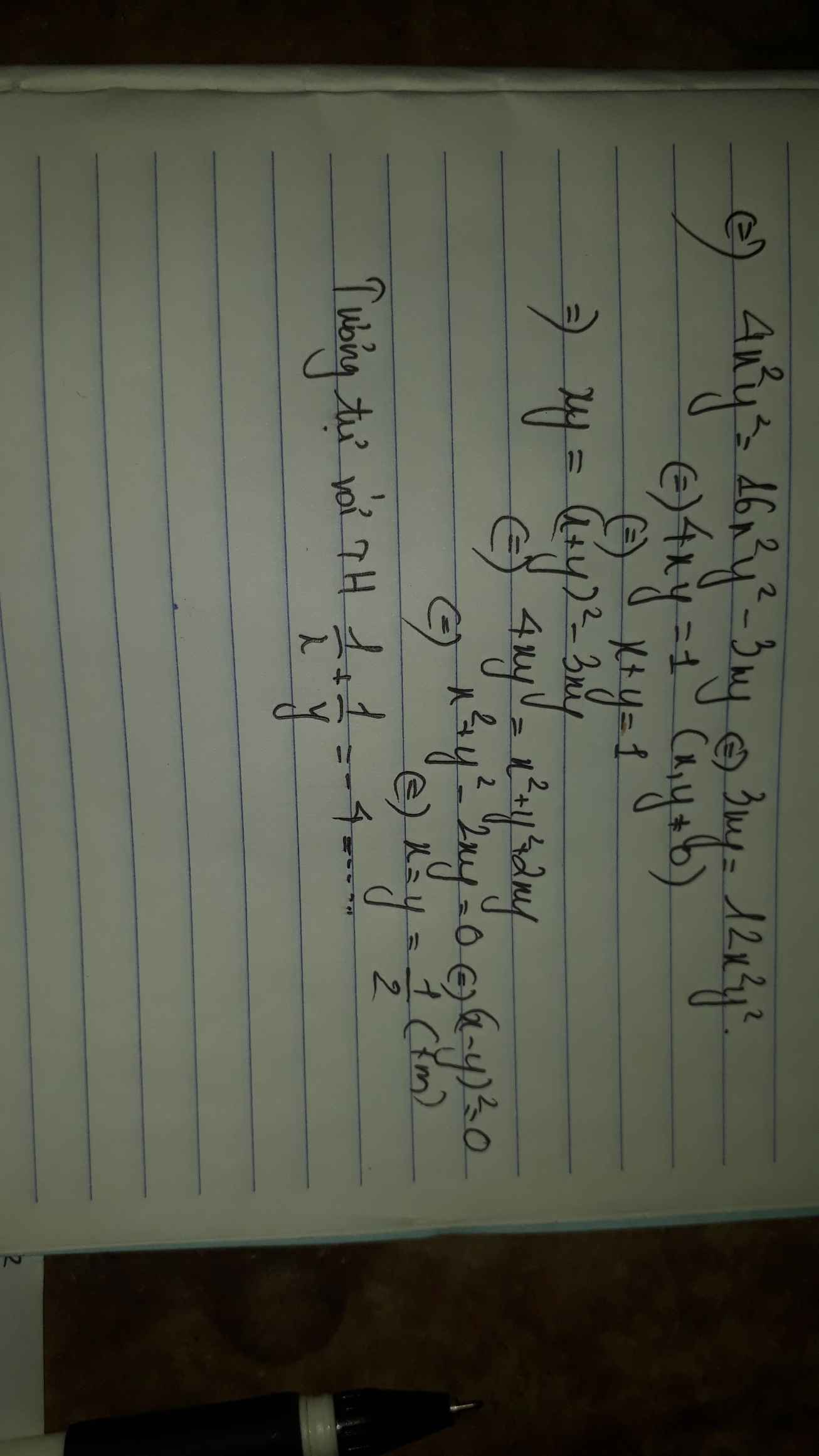a) Sửa đề: \(\dfrac{3}{5x-1}+\dfrac{2}{3-x}=\dfrac{4}{\left(1-5x\right)\left(x-3\right)}\)

ĐKXĐ: \(x\notin\left\{3;\dfrac{1}{5}\right\}\)

Ta có: \(\dfrac{3}{5x-1}+\dfrac{2}{3-x}=\dfrac{4}{\left(1-5x\right)\left(x-3\right)}\)

\(\Leftrightarrow\dfrac{3\left(3-x\right)}{\left(5x-1\right)\left(3-x\right)}+\dfrac{2\left(5x-1\right)}{\left(3-x\right)\left(5x-1\right)}=\dfrac{4}{\left(5x-1\right)\left(3-x\right)}\)

Suy ra: \(9-3x+10x-2=4\)

\(\Leftrightarrow7x+7=4\)

\(\Leftrightarrow7x=-3\)

hay \(x=-\dfrac{3}{7}\)

Vậy: \(S=\left\{-\dfrac{3}{7}\right\}\)

ĐKXĐ: ...

\(\left(\dfrac{x-1}{x+2}\right)^2-4\left(\dfrac{x+2}{x-3}\right)^2+3\left(\dfrac{x-1}{x-3}\right)=0\)

Đặt \(\left\{{}\begin{matrix}\dfrac{x-1}{x+2}=a\\\dfrac{x+2}{x-3}=b\end{matrix}\right.\)

\(\Rightarrow a^2-4b^2+3ab=0\Leftrightarrow\left(a-b\right)\left(a+4b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\a+4b=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x-1}{x+2}-\dfrac{x+2}{x-3}=0\\\dfrac{x-1}{x+2}+\dfrac{4x+8}{x-3}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x-3\right)-\left(x+2\right)^2=0\\\left(x-\right)\left(x-3\right)+4\left(x+2\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow...\)

Giải:

\(\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-3\right)\left(x-2\right)}=\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-1\right)\left(x-4\right)}\)

ĐKXĐ: \(x\ne\left\{1;2;3;4\right\}\)

\(\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-3\right)\left(x-2\right)}=\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-1\right)\left(x-4\right)}\)

\(\Rightarrow\left(x-3\right)\left(x-4\right)+\left(x-1\right)\left(x-4\right)=\left(x-1\right)\left(x-2\right)+\left(x-2\right)\left(x-3\right)\)

\(\Leftrightarrow\left(x-4\right)\left[\left(x-3\right)+\left(x-1\right)\right]=\left(x-2\right)\left[\left(x-1\right)+\left(x-3\right)\right]\)

\(\Leftrightarrow x-4=x-2\)

\(\Leftrightarrow0x=2\)

Vậy ...

\(\dfrac{1}{x+3}+\dfrac{8}{\left(x+1\right)\left(x-3\right)}=\dfrac{2x}{x^2-2x-3}\)

* x² - 2x - 3 = x²- 3x + x - 3 = x(x-3 ) + ( x - 3) = ( x - 3 ) (  x + 1 )

\(\Leftrightarrow\dfrac{1}{x+3}+\dfrac{8}{\left(x+1\right)\left(x-3\right)}=\dfrac{2x}{\left(x-3\right)\left(x+1\right)}\left(ĐKXĐ:x\ne\pm3;x\ne-1\right)\)

\(\Leftrightarrow\left(x+1\right)\left(x-3\right)+8\left(x+3\right)=2x\left(x+3\right)\)

\(\Leftrightarrow x^2-2x+1+8x+24=2x^2+6x\)

\(\Leftrightarrow-x^2+25=0\)

\(\Leftrightarrow x^2-25=0\Leftrightarrow\left(x-5\right)\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-5\end{matrix}\right.\)

Vậy \(S=\left\{-5;5\right\}\)

Ta có: \(\dfrac{\left(x+3\right)\left(x-3\right)}{3}+2=x\left(1-x\right)\)

\(\Leftrightarrow\dfrac{x^2-9}{3}+\dfrac{6}{3}=\dfrac{3x\left(1-x\right)}{3}\)

\(\Leftrightarrow x^2-9+6=3x-3x^2\)

\(\Leftrightarrow x^2-3-3x+3x^2=0\)

\(\Leftrightarrow4x^2-3x-3=0\)

\(\Delta=9-4\cdot4\cdot\left(-3\right)=9+48=57\)

Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là 

\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{57}}{8}\\x_2=\dfrac{3+\sqrt{57}}{8}\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{3-\sqrt{57}}{8};\dfrac{3+\sqrt{57}}{8}\right\}\)

\(ĐK:x\ne2;x\ne-3\\ PT\Leftrightarrow\left(x-2\right)\left(x+3\right)+2\left(x+3\right)=10\left(x-2\right)+50\\ \Leftrightarrow x^2+x-6+2x+6=10x-20+50\\ \Leftrightarrow x^2-13x-30=0\\ \Leftrightarrow x^2-15x+2x-30=0\\ \Leftrightarrow\left(x-15\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=15\\x=-2\end{matrix}\right.\left(tm\right)\)