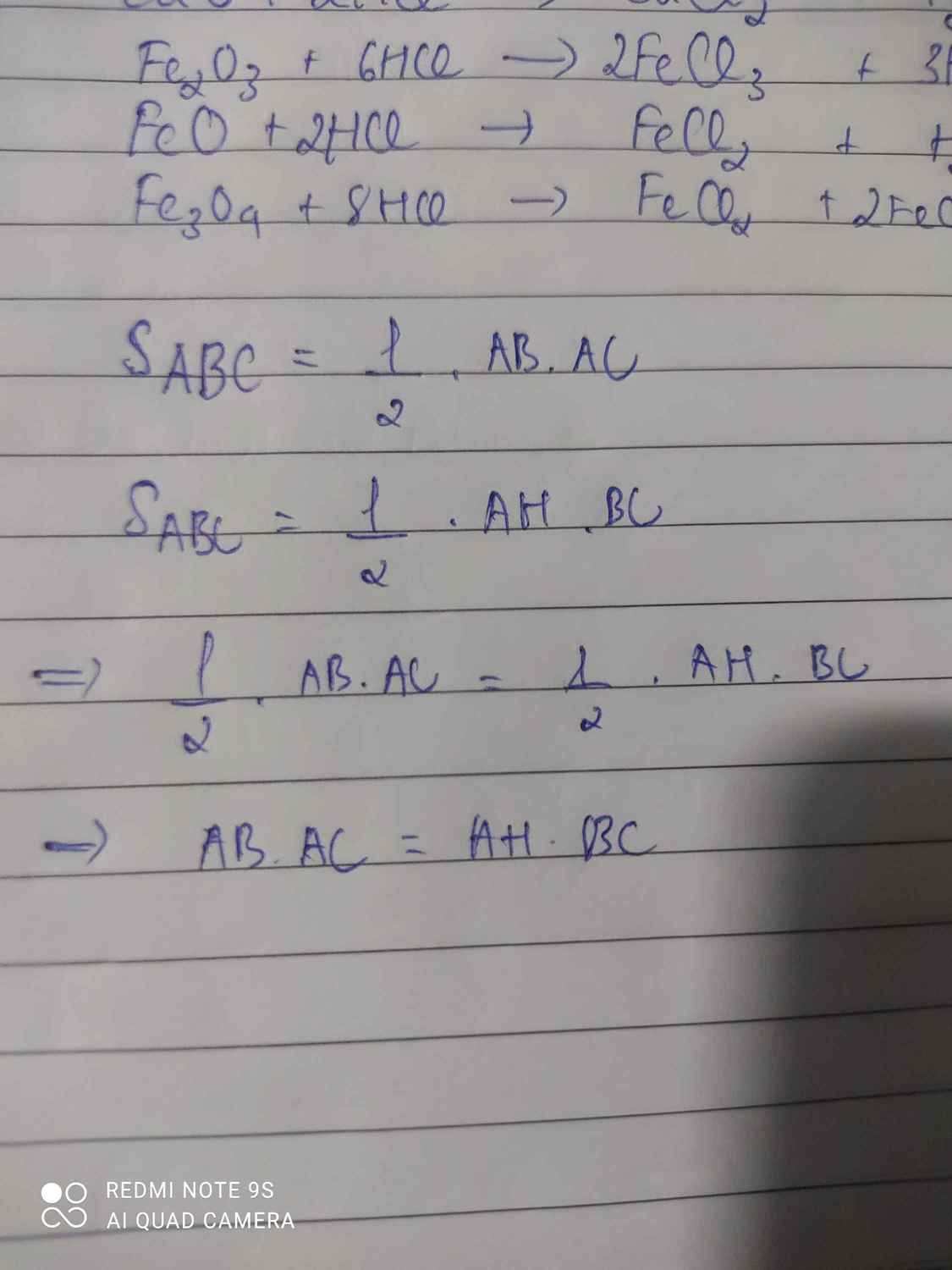Cho △ABC vuông tại A, đường cao AH. Chứng minh: AH+BC >AB+AC

Những câu hỏi liên quan
Cho △ABC vuông tại A có đường cao AH. Chứng minh AB. AC =AH. BC
Cho △ABC vuông tại A có đường cao AH. Chứng minh AB. AC =AH. BC
Cho tam giác ABC vuông tại A đường cao AH, AB=3cm, AC=4cm. a)Chứng minh HBA đồng dạng ABC. b)Tính BC, AH, BH. c)Chứng minh AH=HA.HC
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔHBA\(\sim\)ΔABC(cmt)
nên \(\dfrac{BH}{BA}=\dfrac{BA}{BC}=\dfrac{AH}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{BH}{3}=\dfrac{3}{5}=\dfrac{AH}{4}\)
Suy ra: BH=1,8cm; AH=2,4cm
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a , đường cao ah , chứng minh ab+ac < bc+ah
Ta có: góc ABC = góc BAC + góc ACB (Tam giác abc vuông tại a)
=> BC = AB + AC (Quan hệ giữa góc và cạnh đối diện)
=> BC + AH > AB + AC
Hay AB + AC < BC + AH
Đúng 0
Bình luận (0)
Cho ∆ABC vuông tại A, dựng đường cao AH của ∆ABC.
a) Chứng minh AB. AC = AH. BC.
b) Giả sử AB = 5cm; BC = 13cm. Tính diện tích ∆ABC; AH; BH và AC.
\(a,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}AH\cdot BC\\ \Rightarrow AB\cdot AC=AH\cdot BC\\ b,AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\left(pytago\right)\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot5\cdot12=30\left(cm\right)\\ AH\cdot BC=AB\cdot AC\Rightarrow AH=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\\ BH=\sqrt{AB^2-AH^2}=\dfrac{25}{13}\left(cm\right)\left(pytago\right)\)
Đúng 3
Bình luận (0)
cho △ABC vuông tại A, đường cao AH Chứng minh rằng:
a) △ABC ~ HBAb
) △ABC ~HAC
c) △ HBA~ HAC
d) + AB² =BH.BC
+ AC² = CH. BC
+AB² + AC² = BC²
+AH² = BH. CH
+AH.BC = AB. AC
+ 1/AH² = 1/AB²+ 1/AC²
em cần gấp giúp em với
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
c: ΔABC đồng dạng với ΔHBA
ΔABC đồng dạng với ΔHAC
=>ΔHBA đồng dạng với ΔHAC
d: ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
ΔABC đồng dạng với ΔHAC
=>CA/CH=CB/CA
=>CA^2=CH*CB
Đúng 1
Bình luận (0)
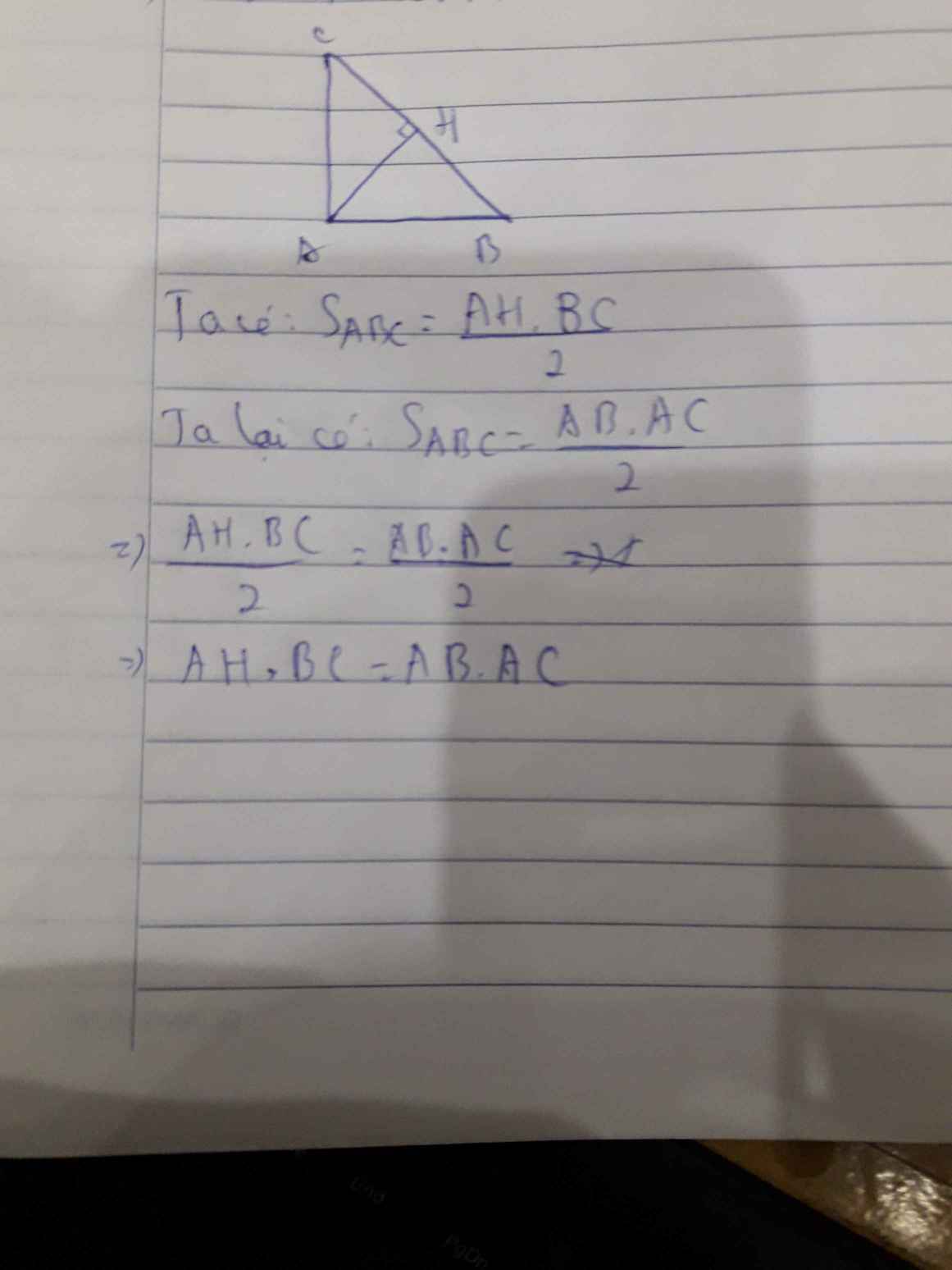
cho tam giac ABC vuông tại A. Kẻ đường cao AH. Chứng minh rằng AH*BC = AB*AC
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{AB\cdot AC}{2}\)
Do đó: \(AH\cdot BC=AB\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng BC + AH > AB + AC
\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH (H thuộc BC)
a) Chứng minh: ABC∽HBA
b)Chứng minh: AH^2 = BH . CH
a, Xét tam giác ABC và tam giác HBA có
^B _ chung ; ^BAC = ^HBA = 900
Vậy tam giác ABC ~ tam giác HBA (g.g)
b, Xét tam giác AHC và tam giác BHA ta có
^AHC = ^BHA = 900
^HAC = ^HBA ( cùng phụ ^HAB )
Vậy tam giác AHC ~ tam giác BHA (g.g)
\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\Rightarrow AH^2=HC.HB\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A với đường cao AH . Chứng minh rằng AH + BC > AB + AC.
Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).
Đúng 0
Bình luận (0)