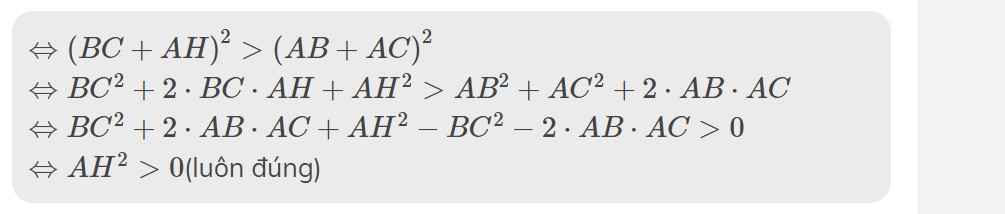Ôn tập Tam giác
Các câu hỏi tương tự
Bài 4 : Cho tam giác ABC vuông tại A ( AB<AC), đường cao AH. giác HAC cắt BC tại E. Vẽ EK vuông góc với AC tại K. Tia phân a) Chứng minh rằng: AAHE = AAKE và AH = AK b) KH cắt AE tại I. Chứng minh rằng: AE I HK từ đó so sánh KE và HI. c) AH cắt KE tại D. Chứng minh rằng: AE L CD. d) Tia phân giác góc ABC cắt AE tại M. Chứng minh rằng: BM // CD
Cho tam giác AbC có góc A = 90°, AC>AB, đường cao AH. a) Biết AB=3cm,AC=4cm. Tính BC, AH b) Lấy điểm D thuộc HC sao cho HD=HB. Chứng minh tam giác ABD cân. c) Kẻ CE vuông góc với AD tại E. Chứng minh góc BAd = góc ACE d) Gọi giao điểm của AH và CE là I. Chứng minh ID_|_AC e) Chứng minh CB là phân giác của góc ACI f) Tính góc BIC
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy D sao cho AD = AH. Gọi E là trung điểm của HD. Tia AE cắt BC tại F. Chứng minh rằng:
𝑎)∆𝐴𝐻𝐸 = ∆𝐴𝐷𝐸; 𝐴𝐸 𝑣𝑢ô𝑛𝑔 𝑔ó𝑐 𝑣ớ𝑖 𝐻𝐷.
b) ∆𝐴𝐻𝐹 = ∆𝐴𝐷𝐹
𝑐)𝐷𝐹𝐶 ̂ = 𝐴𝐵𝐶 ̂
(có vẽ hình)
Cho tam giác ABC vuông tại A. AC>AB. AH là đường cao trong tam giác ABC. Lấy D thuộc tia HC sao cho: HD=HB
a, chứng minh tam giác HAB = tam giác HAD
b, chứng minh AC>CD
c, kẻ CE vuông góc AD (E € AD). Gọi K là giao điểm của AH và CE. Chứng minh: KD // AB
d, chứng minh DH là đường trung trực của AK
e, giả sử góc B = 60°. Chứng minh HC = 3HB
Cho tam giác ABC vuông tại A .Đường phân giác của góc B cắt AC tại E.Kẻ EH vuông góc với BC (H thuộc BC) . a/ Chứng minh tam giác ABE = tam giác HBE b/ Chứng minh BE là đường trung trực của đoạn thẳng AH. c/ Gọi I là giao điểm của Be và AH .Cho AB = 10 cm, AH = 16 cm và G là trọng tâm của tam giác ABH. Tính BG. d/ Gọi K là giao điểm của AB và EH. Chứng minh tam giác BCK cân.
Cho tam giác ABC vuông tại A , kẻ đường cao AH . trên cạnh AC lấy điểm K sao cho AK = AH . kẻ KD vuông góc với AC tại K ( D thuộc BC ) > chứng minh
a, tam giác AHD = tam giác AKD
b, AD là đường trung trực của đoạn thẳng AK
Cho tam giác ABC cân tại A, đường cao AH (H thuộc BC).
a) Chứng minh △AHB=△AHC.
b) Từ H kẻ đường thẳng song song với AC, cắt AB tại D. Chứng minh AD=DH.
c) Gọi E là trung điểm AC, CD cắt AH tại G. Chứng minh B,G, E thẳng hàng.
d) Chứng minh chu vi △ABC > AH+3BG.
Cho tam giác ABC cân tại A có A90 độ. Kẻ AH vuông góc với BC. Qua H kẻ đường thẳng song song với AC, đường thẳng này cắt AB tại D.a,Cho AH 12 cm, AC 13cm. Tính HCb, Chứng minh tam giác ABH và tam giác ACH ;c, Chứng minh là góc tù; Từ đó so sánh HA và DA ;d,Chứng minh tam giác ADH là tam giác cân tại D;e, AH cắt CD tại G; chứng minh AG2GH ;g, Chứng minh chu vi tam giác ABC lớn hơn tổng AH 3BG
Đọc tiếp
Cho tam giác ABC cân tại A có A<90 độ. Kẻ AH vuông góc với BC. Qua H kẻ đường thẳng song song với AC, đường thẳng này cắt AB tại D.
a,Cho AH =12 cm, AC =13cm. Tính HC
b, Chứng minh tam giác ABH và tam giác ACH ;
c, Chứng minh là góc tù; Từ đó so sánh HA và DA ;
d,Chứng minh tam giác ADH là tam giác cân tại D;
e, AH cắt CD tại G; chứng minh AG=2GH ;
g, Chứng minh chu vi tam giác ABC lớn hơn tổng AH 3BG
ABC cân tại A, góc A 500:a) Tính góc B, góc C?b) Vẽ AH vuông góc với BC (H thuộc BC). Chứng minh ABHACH.c) Biết AB 17cm, BC 16cm, tính AH?Vẽ CN vuông góc AB (N thuộc AB), BM vuông góc AC (M thuộc AC). Chứng minh NC MB.
Đọc tiếp
ABC cân tại A, góc A = 500:
a) Tính góc B, góc C?
b) Vẽ AH vuông góc với BC (H thuộc BC). Chứng minh ![]() ABH=
ABH=![]() ACH.
ACH.
c) Biết AB = 17cm, BC = 16cm, tính AH?
Vẽ CN vuông góc AB (N thuộc AB), BM vuông góc AC (M thuộc AC). Chứng minh NC = MB.