làm hộ mk bài 2vs 3 nha xin cảm ơn
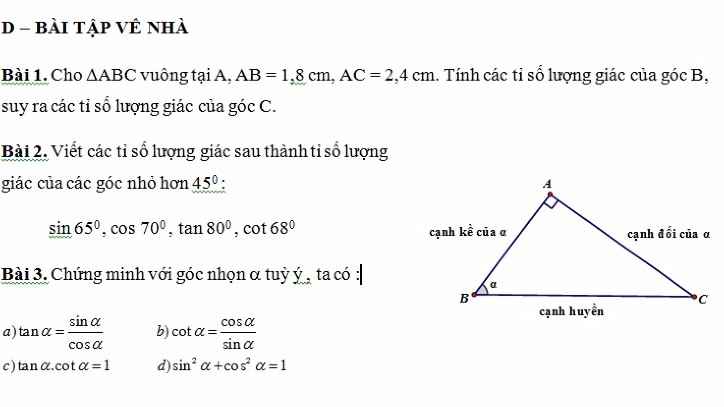
 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều![]()
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
Bài 5:a)
Xét tam giác vuông $AHB$ và $AHC$ có:
$AB=AC$ (do $ABC$ là tam giác cân ở A)
$\widehat{ABH}=\widehat{ACH}$ (do tam giác $ABC$ cân ở A)
$\Rightarrow \triangle AHB=\triangle AHC$ (cạnh huyền- góc nhọn)
$\Rightarrow HB=HC$ và $\widehat{BAH}=\widehat{CAH}$ (đpcm)
b)
$HB=HC$ nên $H$ là trung điểm $BC$. Do đó $HB=BC:2=4$ (cm)
Áp dụng định lý Pitago:
$AH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)
c)
Xét tam giác vuông $ADH$ và $AEH$ có:
$AH$ chung
$\widehat{DAH}=\widehat{EAH}$ (do $\widehat{BAH}=\widehat{CAH}$)
$\Rightarrow \triangle ADH=\triangle AEH$ (cạnh huyền- góc nhọn)
$\Rightarrow DH=EH$ nên tam giác $HDE$ cân tại $H$.
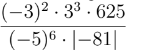 cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !
cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !
\(\dfrac{\left(-3\right)^2.3^3.625}{\left(-5\right)^6.\left|-81\right|}=\dfrac{3^2.3^3.5^4}{5^6.81}=\dfrac{3^5.5^4}{5^6.3^4}=\dfrac{3}{5^2}=\dfrac{3}{25}\)
cảm ơn mọi người đã hộ trợ mình làm những bài khó này.
em xin cảm ơn.
1 lần nữa em xin trân trọng cảm ơn.
Tìm x,y thuộc Z
1/x=y/-5
Làm hộ mk bài này nha!Cảm ơn mn nhìu:3:3:3
\(\frac{1}{x}=\frac{y}{-5}\)
\(\Leftrightarrow x\cdot y=1\cdot\left(-5\right)=-5\)
Mà x,y thuộc Z
\(\Rightarrow x\inƯ\left(-5\right)=\left\{-5;-1;1;5\right\}\)
Lập bảng
| x | -5 | -1 | 1 | 5 |
| y | -1 | -5 | 5 | 1 |
| KL | c | c | c | c |
Vậy (x;y)=(-5;-1);(-1;-5);(1;5);(5;1)
[Cầu Tràng Tiền ở Huế được bắc qua sông .....................] làm hộ mình câu này mk ko bít nhìu về câu này nếu có thể các bạn gửi mk xem ảnh nha cảm ơn các bạn và xin lỗi đã làm phiền
Cầu Tràng Tiền ở Huế được bắc qua sông Hương nha bạn ![]()
cảm ơn đáp án của các bạn nha 💞"thành thật cảm ơn" 💖

Làm hết hộ em nha em xin cảm ơn ạ
Bạn thể tự viết ra bởi vì mỗi người có những ý kiến khác nhau
mn giải thích hộ mk cách lm bài 6 với ạ , mk xin trân thành cảm ơn ạ 
a: Ta có: \(\dfrac{n\left(n+1\right)}{2}=231\)
\(\Leftrightarrow n^2+n-462=0\)
\(\Leftrightarrow n^2+22n-21n-462=0\)
\(\Leftrightarrow\left(n+22\right)\left(n-21\right)=0\)
\(\Leftrightarrow n=21\)
1 + 2 + 3 + 4 + ...... n = 231
n =
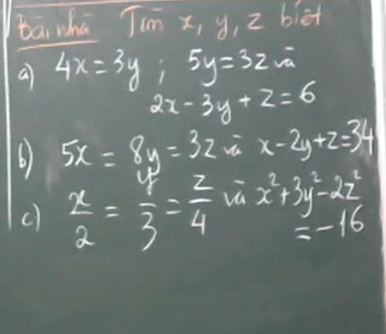
Làm hết hộ em nha! Em xin cảm ơn mọi người nhiều ạ!
Lời giải:
a.
$4x=3y\Rightarrow 20x=15y$
$5y=3z\Rightarrow 15y=9z$
$\Rightarrow 20x=15y=9z=t$
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{15}; z=\frac{t}{9}$
Khi đó:
$2x-3y+z=\frac{2t}{20}-\frac{3t}{15}+\frac{t}{9}=5$
$\frac{t}{90}=6$
$t=540$
$x=\frac{540}{20}=27; y=\frac{540}{15}=36;z=\frac{540}{9}=60$
b. Đặt $5x=8y=3z=t$
$\Rightarrow x=\frac{t}{5}; y=\frac{t}{8}; z=\frac{t}{3}$
Khi đó:
$x-2y+z=34$
$\frac{t}{5}-\frac{2t}{8}+\frac{t}{3}=34$
$\frac{17}{60}t=34$
$t=120$
$x=\frac{120}{5}=24; y=\frac{120}{8}=15; z=\frac{120}{3}=40$
c.
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+3y^2-2z^2=-16$
$(2t)^2+3(3t)^2-2(4t)^2=-16$
$-t^2=-16$
$t^2=16$
$t=\pm 4$
Khi $t=4$ thì $x=2.4=8; y=3.4=12; z=4.4=16$
Khi $t=-4$ thì $x=-8; y=-12; z=-16$
b: Ta có: \(5x=8y=3z\)
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{5}}=\dfrac{y}{\dfrac{1}{8}}=\dfrac{z}{\dfrac{1}{3}}\)
hay \(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}\)
mà x-2y+z=34
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{5}}=\dfrac{2y}{\dfrac{1}{4}}=\dfrac{z}{\dfrac{1}{3}}=\dfrac{x-2y+z}{\dfrac{1}{5}-\dfrac{1}{4}+\dfrac{1}{3}}=\dfrac{34}{\dfrac{17}{60}}=120\)
Do đó: x=24; y=15; z=40