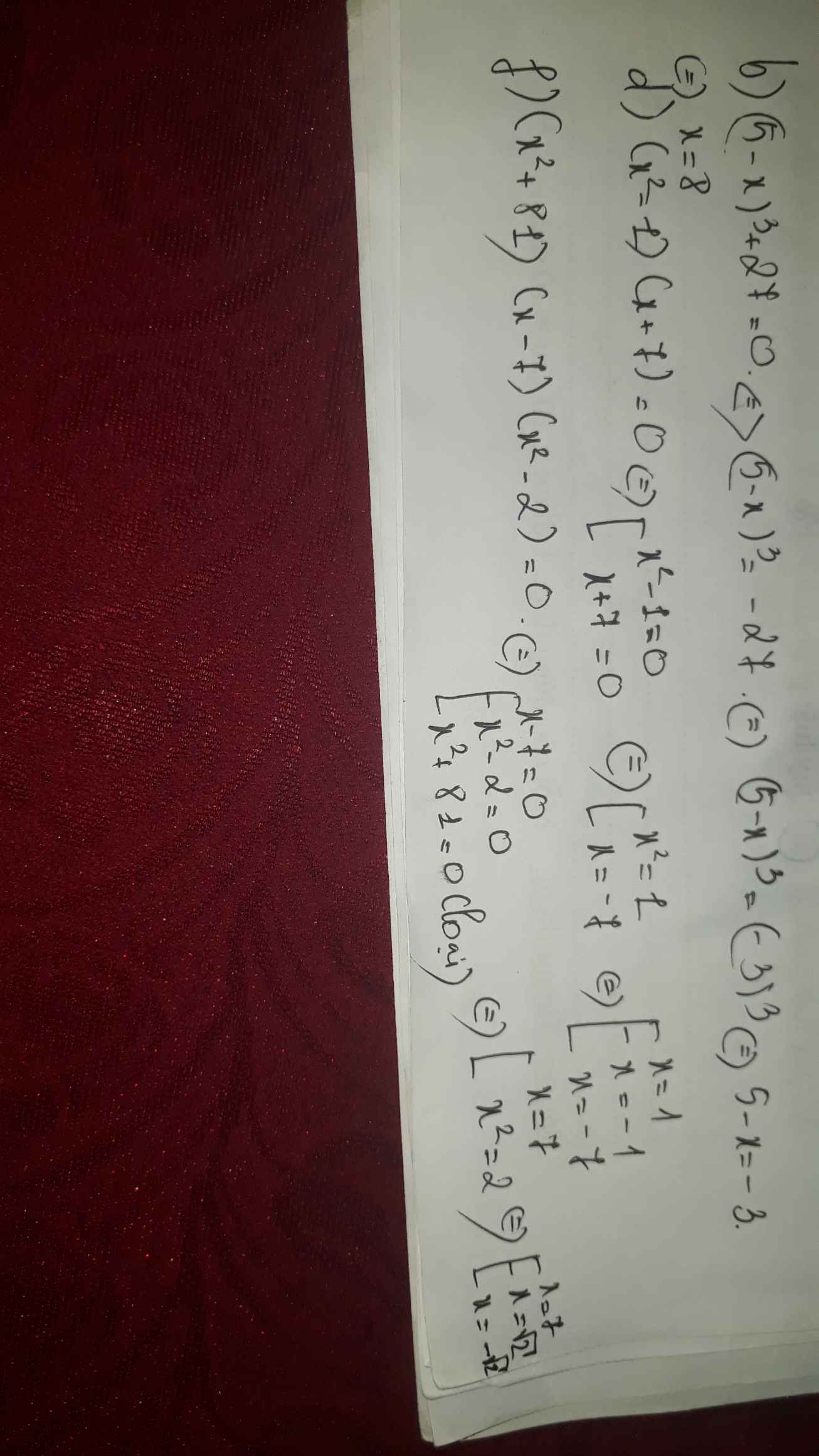\(\left|x+1\right|+\left|x+2\right|=0\)

Những câu hỏi liên quan
i, \(\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\)
k, \(\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\)
l, \(\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\)
\(\left(x-1\right)\left(-x+2\right)=0\Leftrightarrow x=1;x=2\)
\(\left(x+2\right)\left(x+1-x+3\right)=0\Leftrightarrow x=-2\)
\(\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(2x+5\right)=0\Leftrightarrow\left(x-2\right)\left(-x-2\right)=0\Leftrightarrow x=-2;x=2\)
Đúng 4
Bình luận (0)
\(i,\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(-x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\ k,\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+1-x+3\right)=0\\ \Leftrightarrow4\left(x+2\right)=0\\ \Leftrightarrow x+2=0\\ \Leftrightarrow x=-2\\ l,\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\\ \Leftrightarrow\left(x-2\right)\left(2x+5\right)-\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+5-x-3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm x:8) 1-left(x-6right)4left(2-2xright)9)left(3x-2right)left(x+5right)010)left(x+3right)left(x^2+2right)011)left(5x-1right)left(x^2-9right)012)xleft(x-3right)+3left(x-3right)013)xleft(x-5right)-4x+20014)x^2+4x-50
Đọc tiếp
Tìm \(x\):
\(8\)) \(1-\left(x-6\right)=4\left(2-2x\right)\)
\(9\))\(\left(3x-2\right)\left(x+5\right)=0\)
\(10\))\(\left(x+3\right)\left(x^2+2\right)=0\)
\(11\))\(\left(5x-1\right)\left(x^2-9\right)=0\)
\(12\))\(x\left(x-3\right)+3\left(x-3\right)=0\)
\(13\))\(x\left(x-5\right)-4x+20=0\)
\(14\))\(x^2+4x-5=0\)
\(8,1-\left(x-6\right)=4\left(2-2x\right)\)
\(\Leftrightarrow1-x+6=8-8x\)
\(\Leftrightarrow-x+8x=8-1-6\)
\(\Leftrightarrow7x=1\)
\(\Leftrightarrow x=\dfrac{1}{7}\)
\(9,\left(3x-2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-5\end{matrix}\right.\)
\(10,\left(x+3\right)\left(x^2+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\varnothing\end{matrix}\right.\)
Đúng 2
Bình luận (0)
`8)1-(x-5)=4(2-2x)`
`<=>1-x+5=8-6x`
`<=>5x=2<=>x=2/5`
`9)(3x-2)(x+5)=0`
`<=>[(x=2/3),(x=-5):}`
`10)(x+3)(x^2+2)=0`
Mà `x^2+2 > 0 AA x`
`=>x+3=0`
`<=>x=-3`
`11)(5x-1)(x^2-9)=0`
`<=>(5x-1)(x-3)(x+3)=0`
`<=>[(x=1/5),(x=3),(x=-3):}`
`12)x(x-3)+3(x-3)=0`
`<=>(x-3)(x+3)=0`
`<=>[(x=3),(x=-3):}`
`13)x(x-5)-4x+20=0`
`<=>x(x-5)-4(x-5)=0`
`<=>(x-5)(x-4)=0`
`<=>[(x=5),(x=4):}`
`14)x^2+4x-5=0`
`<=>x^2+5x-x-5=0`
`<=>(x+5)(x-1)=0`
`<=>[(x=-5),(x=1):}`
Đúng 1
Bình luận (0)
\(11,=>\left[{}\begin{matrix}5x-1=0\\x^2-9=0\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\\x=-3\end{matrix}\right.\\ 12,=>\left(x+3\right)\left(x-3\right)=0\\ =>\left[{}\begin{matrix}x+3=0\\x-3=0\end{matrix}\right.=>\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\\ 13,=>x\left(x-5\right)-4\left(x-5\right)=0\\ =>\left(x-4\right)\left(x-5\right)=0\\ =>\left[{}\begin{matrix}x-4=0\\x-5=0\end{matrix}\right.=>\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
\(14,=>x^2+5x-x-5=0\\ =>x\left(x+5\right)-\left(x+5\right)=0\\ =>\left(x-1\right)\left(x+5\right)=0\\ =>\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.=>\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
left(x^2-x+1right)^4-6x^2left(x^2-x+1right)^2+5x^40
Leftrightarrowleft[left(x^2-x+1right)^2right]^2-2left(x^2-x+1right)^2.3x^2+left(3x^2right)^2-4x^40
Leftrightarrowleft[left(x^2-x+1right)^2-3x^2right]^2-left(2x^2right)^20
Leftrightarrowleft[left(x^2-x+1right)^2-3x^2+2x^2right]left[left(x^2-x+1right)^2-3x^2-2x^2right]0
Leftrightarrowleft[left(x^2-x+1right)^2-x^2right]left[left(x^2-x+1right)^2-5x^2right]0
Leftrightarrowleft(x^2-x+1+x^2right)left(x^2-x+1-x^2right)left(x^4-2x^3-4x^2+1right)0...
Đọc tiếp
\(\left(x^2-x+1\right)^4-6x^2\left(x^2-x+1\right)^2+5x^4=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2\right]^2-2\left(x^2-x+1\right)^2.3x^2+\left(3x^2\right)^2-4x^4=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-3x^2\right]^2-\left(2x^2\right)^2=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-3x^2+2x^2\right]\left[\left(x^2-x+1\right)^2-3x^2-2x^2\right]=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-x^2\right]\left[\left(x^2-x+1\right)^2-5x^2\right]=0\)
\(\Leftrightarrow\left(x^2-x+1+x^2\right)\left(x^2-x+1-x^2\right)\left(x^4-2x^3-4x^2+1\right)=0\)
\(\Leftrightarrow\left(2x^2-x+1\right)\left(1-x\right)\left(x+1\right)\left(x^3-2x^2-x+1\right)=0\)
Mấy bạn cho mình gửi tạm nha, xíu mình nhờ CTV xóa :(
Giải các phương trình sau:
a \(\left(x+2\right)\left(x+\text{4}\right)\left(x+6\right)\left(x+8\right)+16=0\)
b \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)
c \(\left(4x+1\right)\left(12x-1\right)\left(3x+2\right)\left(x+1\right)-4=0\)
d \(\left(x^2-3x+2\right)\left(x^2+15x+56\right)+8=0\)
b: Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24=0\)
\(\Leftrightarrow x^2+7x+6=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-6\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1) \(\left(3-x^2\right)+6-2x=0\)
2) \(5\left(2x-1\right)+7=4\left(2-x\right)+2\)
3) \(x^2-6x+4\left(x-6\right)=0\)
4) \(\left(x+1\right)\left(2x-3\right)=x\left(x+1\right)\)
1) Ta có: \(\left(3-x^2\right)+6-2x=0\)
\(\Leftrightarrow3-x^2+6-2x=0\)
\(\Leftrightarrow-x^2-2x+9=0\)
\(\Leftrightarrow x^2+2x-9=0\)
\(\Leftrightarrow x^2+2x+1=10\)
\(\Leftrightarrow\left(x+1\right)^2=10\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=\sqrt{10}\\x+1=-\sqrt{10}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{10}-1\\x=-\sqrt{10}-1\end{matrix}\right.\)
Vậy: \(S=\left\{\sqrt{10}-1;-\sqrt{10}-1\right\}\)
Đúng 2
Bình luận (0)
2) Ta có: \(5\left(2x-1\right)+7=4\left(2-x\right)+2\)
\(\Leftrightarrow10x-5+7=8-4x+2\)
\(\Leftrightarrow10x+4x=8+2+5-7\)
\(\Leftrightarrow14x=8\)
\(\Leftrightarrow x=\dfrac{4}{7}\)
Vậy: \(S=\left\{\dfrac{4}{7}\right\}\)
Đúng 2
Bình luận (0)
3) Ta có: \(x^2-6x+4\left(x-6\right)=0\)
\(\Leftrightarrow x\left(x-6\right)+4\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)
Vậy: S={6;-4}
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
\(\frac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\frac{x\left(x-3\right)}{2\left(x-3\right)\left(x+1\right)}-\frac{4x}{2\left(x-3\right)\left(x+1\right)}=0\)
\(\frac{x^2+x+x^2-3x-4x}{2\left(x-3\right)\left(x+1\right)}=0\)
\(x^2-3x=0\)
đâu phải toán lớp 1
bạn chọn nhầm à
Tìm x, biết : a/ dfrac{1}{3}xleft(x^2-4right)0b/ xleft(x+5right)x+5c/ x^3-dfrac{1}{9}x03)^2-left(x+5right)^20e/ left(x+2right)^2-left(x-2right)left(x+2right)0f/ xleft(2x-3right)-6+4x0g/ 2left(3x-2right)^2-9x^2+40h/ x^2left(x+1right)+2xleft(x+1right)0i/ 4x^2+9x+50
Đọc tiếp
Tìm x, biết :
a/ \(\dfrac{1}{3}x\left(x^2-4\right)=0\)
b/ \(x\left(x+5\right)=x+5\)
c/ \(x^3-\dfrac{1}{9}x=0\)
3)\(^2-\left(x+5\right)^2=0\)
e/ \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
f/ \(x\left(2x-3\right)-6+4x=0\)
g/ \(2\left(3x-2\right)^2-9x^2+4=0\)
h/ \(x^2\left(x+1\right)+2x\left(x+1\right)=0\)
i/ \(4x^2+9x+5=0\)
a) \(\Rightarrow\dfrac{1}{3}x\left(x-2\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow\left(x+5\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)
c) \(\Rightarrow x\left(x^2-\dfrac{1}{9}\right)=0\Rightarrow x\left(x-\dfrac{1}{3}\right)\left(x+\dfrac{1}{3}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
e) \(\Rightarrow\left(x+2\right)\left(x+2-x+2\right)=0\Rightarrow\left(x+2\right).4=0\Rightarrow x=-2\)
f) \(\Rightarrow x\left(2x-3\right)+2\left(2x-3\right)=0\Rightarrow\left(2x-3\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\)
g) \(\Rightarrow2\left(3x-2\right)^2-\left(3x-2\right)\left(3x+2\right)=0\Rightarrow\left(3x-2\right)\left(3x-6\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
h) \(\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)
i) \(\Rightarrow4x\left(x+1\right)+5\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(4x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải các phương trình sau
1. \(\left(x-1\right)\left(x+5\right)\left(x^2+4x+8\right)+40=0\)
2. \(\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)-15=0\)
A)left(2x-7right)^2-6left(2x-7right)left(x-3right)0B) x^3+1+left(x^2-x+1right)0C) left(3x+1right)^2-x^2+8x-160D)left(x+1right)left(x-1right)^2left(x+1right)left(x-2right)^20E) left(3x+1right)left(x-3right)^2left(3x+1right)left(2x-5right)^2F) left(x+5right)left(3x+2right)^2x^2left(x+5right)
Đọc tiếp
A)\(\left(2x-7\right)^2-6\left(2x-7\right)\left(x-3\right)=0\)
B) \(x^3+1+\left(x^2-x+1\right)=0\)
C) \(\left(3x+1\right)^2-x^2+8x-16=0\)
D)\(\left(x+1\right)\left(x-1\right)^2\left(x+1\right)\left(x-2\right)^2=0\)
E) \(\left(3x+1\right)\left(x-3\right)^2=\left(3x+1\right)\left(2x-5\right)^2\)
F) \(\left(x+5\right)\left(3x+2\right)^2=x^2\left(x+5\right)\)
\(Bài\) \(2:\) \(Tìm\) \(x:\)
b) \(\left(5-x\right)^3+27=0\)
d) \(\left(x^2-1\right).\left(x+7\right)=0\)
f) \(\left(x^2+81\right).\left(x-7\right).\left(x^2-2\right)=0\)
b) Ta có: \(\left(5-x\right)^3+27=0\)
\(\Leftrightarrow\left(5-x\right)^3=-27\)
\(\Leftrightarrow5-x=-3\)
hay x=8
d) Ta có: \(\left(x^2-1\right)\left(x+7\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=-7\end{matrix}\right.\)
f) Ta có: \(\left(x^2+81\right)\left(x-7\right)\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+\sqrt{2}\right)\left(x-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)