cho hình vẽ , tính widehat{MHx} + widehat{MQy} ( xHQ; HEM; HQy; HMQ đều là góc vuông)
Đọc tiếp
cho hình vẽ , tính \(\widehat{MHx}\) + \(\widehat{MQy}\) ( xHQ; HEM; HQy; HMQ đều là góc vuông)
Những câu hỏi liên quan
6 tháng 10 2021 lúc 13:30
Cho hình vẽ, biết rằng CD//Eywidehat{BAx} 1400 , widehat{ABD} 400 , widehat{BEy} 1300a, tính widehat{CBE} ?b, chứng minh Ax // Eyc, chứng minh ABperpBE thêm vào hình vẽ: widehat{B_1} 400, widehat{A_1} 1400 , widehat{E_1} 1300A x y E B C D
Đọc tiếp
Cho hình vẽ, biết rằng CD//Ey
\(\widehat{BAx}\)= 1400 , \(\widehat{ABD}\)= 400 , \(\widehat{BEy}\)= 1300
a, tính \(\widehat{CBE}\) ?
b, chứng minh Ax // Ey
c, chứng minh AB\(\perp\)BE thêm vào hình vẽ: \(\widehat{B_1}\)= 400, \(\widehat{A_1}\)= 1400 , \(\widehat{E_1}\)= 1300
A x y E B C D
a) Ta có: CD//Ey
\(\Rightarrow\widehat{CBE}=\widehat{E_1}=130^0\)(so le trong)
b) Ta có: Ta có: CD//Ey
\(\Rightarrow\widehat{EBD}+\widehat{E_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{EBD}=180^0-\widehat{E_1}=50^0\)
Ta có: \(\widehat{EBD}+\widehat{B_1}=50^0+40^0=90^0\)
=> AB⊥BE
Đúng 0
Bình luận (0)
8 tháng 10 2021 lúc 8:26
1. Cho hình vẽ , biết a // b ; \(\widehat{ACB}\) = 37'( độ ) , \(\widehat{D_1}\) = 45'( độ ) . Tính \(\widehat{ABC}\) , \(\widehat{AED}\)
8 tháng 10 2021 lúc 8:28
1. Cho hình vẽ , biết a // b ; widehat{ACB} 37( độ ) , widehat{D_1} 45( độ ) . Tính widehat{ABC} , widehat{AED}
Đọc tiếp
1. Cho hình vẽ , biết a // b ; \(\widehat{ACB}\) = 37'( độ ) , \(\widehat{D_1}\) = 45'( độ ) . Tính \(\widehat{ABC}\) , \(\widehat{AED}\)
Cho hình vẽ dưới đây biết a // (song song) b và widehat{M1} - widehat{N2} 50◦ Tính widehat{M2} và widehat{N2}
Đọc tiếp
Cho hình vẽ dưới đây biết a // (song song) b và \(\widehat{M1} - \widehat{N2}\) = 50◦
Tính \(\widehat{M2} và \widehat{N2}\)
8 tháng 10 2021 lúc 8:47
1. Cho hình vẽ , biếta // b ; c ⊥ a và widehat{DCB} 30( độ ) . Tính widehat{D_1} và widehat{B_2}
Đọc tiếp
1. Cho hình vẽ , biết
a // b ; c ⊥ a và \(\widehat{DCB}\) = 30'( độ ) . Tính \(\widehat{D_1}\) và \(\widehat{B_2}\)
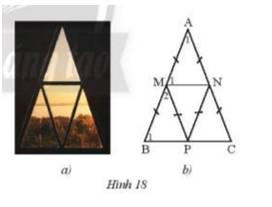
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
Đúng 0
Bình luận (0)
Cho hình vẽ: (hình minh họa)
ababxyABxyCD60*
Biết text{ }widehat{text{aAB}} widehat{text{ABC}} ; widehat{text{aDC}} 60^{ }độ
a) Chứng minh aa // bb
b) Tính số đo widehat{text{bCy}}, widehat{text{DCb}}
c) Gọi Dm là tia phân giác của widehat{text{aDC}}, Cn là tia phân giác của widehat{text{bCy}}. Chứng minh Dm//Cn
Đọc tiếp
Cho hình vẽ: (hình minh họa)
Biết \(\text{ }\widehat{\text{aAB}}\) = \(\widehat{\text{ABC}}\) ; \(\widehat{\text{a'DC}}\) = 60\(^{ }\)độ
a) Chứng minh aa' // bb'
b) Tính số đo \(\widehat{\text{b'Cy'}}\), \(\widehat{\text{DCb'}}\)
c) Gọi Dm là tia phân giác của \(\widehat{\text{a'DC}}\), Cn là tia phân giác của \(\widehat{\text{b'Cy'}}\). Chứng minh Dm//Cn
18 tháng 3 2021 lúc 20:39
Cho \(\widehat{aOb}\)\(=120^o\).Vẽ tia \(Oc\) trong góc đó sao cho \(\widehat{aOc}\)\(=50^o\).Vẽ tia phân giác \(Om\)của \(\widehat{bOc}\).Tính :
a)Tính \(\widehat{bOm}\)
b)Tính \(\widehat{aOm}\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOc}< \widehat{aOb}\left(50^0< 120^0\right)\)
nên tia Oc nằm giữa hai tia Oa và Ob
\(\Leftrightarrow\widehat{aOc}+\widehat{bOc}=\widehat{aOb}\)
\(\Leftrightarrow\widehat{bOc}=\widehat{aOb}-\widehat{aOc}=120^0-50^0=70^0\)
Ta có: Om là tia phân giác của \(\widehat{bOc}\)(gt)
nên \(\widehat{bOm}=\dfrac{\widehat{bOc}}{2}=\dfrac{70^0}{2}\)
hay \(\widehat{bOm}=35^0\)
Vậy: \(\widehat{bOm}=35^0\)
Đúng 1
Bình luận (0)
Cho hình vẽ biết Ax // Ny // Dz
\(\widehat{xMN}=50^o,\)\(\widehat{MND}=120^o\). Tính \(\widehat{MND,}\widehat{NDz}\)
Cho hình vẽ , biết :
\(\widehat{MNP}+\widehat{NPQ}=180^0;\widehat{MPQ}=50^0;Qx\perp PQ\)
Tính góc NMP và NRx