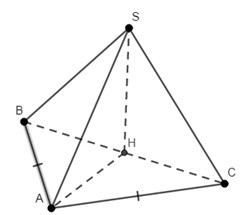
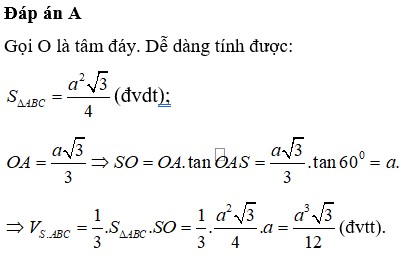Cho hinh chop deu Sabc có cạnh bên bằng a và hợp vs đáy 1 góc 60 độ. Tính Vabc?

Những câu hỏi liên quan
Cho hình chóp đều sabc có cạnh đáy bằng a, góc giữa một mặt bên và mặt đáy bằng 60 độ. Tính độ dài đường cao sh của hình chóp?
Xem chi tiết
Lời giải:
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$
Đúng 1
Bình luận (1)
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
60
°
. Tính thể tích của khối chóp SABC A.
a
3
3
12
B.
a
3
12
C.
a
3
3
4...
Đọc tiếp
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính thể tích của khối chóp SABC
A. a 3 3 12
B. a 3 12
C. a 3 3 4
D. a 3 3 36
Tính thể tích tứ diện SABC trong mỗi trường hợp sau :a, SABC là hình chóp đều, cạnh đáya, góc giữa mặt bên và cạnh đáy 45 độ.b,Các cạnh bên cùng tạo với đáy góc 60 độ, AB5a, BC6a, CA7a.c, mp(SAB) vuông góc với mp(ABC), tam giác ABC là tam giác đều có cạnha, góc giữa SC và mp(ABC)30 độ.d,góc giữa các mặt bên và mặt đáy nhau60 độ, tam giác ABC có ABa,AC2a, góc A60 độ .e, SA vuông góc với mp(ABC), SAa, góc giữa (SBC) và đáy là 60 độ
Đọc tiếp
Tính thể tích tứ diện SABC trong mỗi trường hợp sau :
a, SABC là hình chóp đều, cạnh đáy=a, góc giữa mặt bên và cạnh đáy =45 độ.
b,Các cạnh bên cùng tạo với đáy góc 60 độ, AB=5a, BC=6a, CA=7a.
c, mp(SAB) vuông góc với mp(ABC), tam giác ABC là tam giác đều có cạnh=a, góc giữa SC và mp(ABC)=30 độ.
d,góc giữa các mặt bên và mặt đáy = nhau=60 độ, tam giác ABC có AB=a,AC=2a, góc A=60 độ .
e, SA vuông góc với mp(ABC), SA=a, góc giữa (SBC) và đáy là 60 độ
cho hình chóp tam giác đều SABC có cạnh đáy bằng a cạnh bên hợp với đáy một góc 60 độ hình nón tròn xoay có đỉnh s đáy là đường tròn ngoại tiếp tam giác ABC có diện tích xung quanh là
Xem chi tiết
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow\widehat{SAO}=60^0\)
\(AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(S_{xq}=\pi.AO.SA=\dfrac{2\pi a^2}{3}\)
Đúng 2
Bình luận (0)
cho hinh chóp đều SABC đường cao SO vuông góc với đáy canh bên bằng b góc giữa mặt bên và mặt đáy bằng 60 độ.tính thể tích SABC
Cho hình chóp đều SABC. Cạnh đáy bằng a. Tâm O. Góc giữa mặt bên và đáy bằng 60°. Tính khoảng cách a)O đến (SAC) b)B đến (SAC)
Vì SABC là hình chóp đều nên nó sẽ có tính đối xừng, và cách làm giống bài bên trên toi vừa làm, bạn tham khảo
Đúng 1
Bình luận (0)
Cho hình chóp SABC có đáy là tam giác vuông cân tại A, BC2a, góc giữa các cạnh bên và mặt đáy bằng
60
°
. Hỏi thể tích của khối chóp SABC bằng bao nhiêu? A.
a
3
2
B.
a
3
3
3
C.
2
a
3
2
C.
3
a
3...
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác vuông cân tại A, BC=2a, góc giữa các cạnh bên và mặt đáy bằng 60 ° . Hỏi thể tích của khối chóp SABC bằng bao nhiêu?
A. a 3 2
B. a 3 3 3
C. 2 a 3 2
C. 3 a 3 3
Cho hình chóp SABC có các cạnh bên nghiêng đều trên đáy một góc 60 độ. Biết tam giác ABC có AB=a, AC=2a, BC=5a/2. Tính thể tích khối chóp SABC
Gọi H là hình chiếu vuông góc của S lên đáy
\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=60^0\)
\(\Rightarrow AH=BH=CH=\dfrac{SH}{tan60^0}\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác đáy
\(\Rightarrow AH=R=\dfrac{AB.BC.AC}{4S_{ABC}}\)
\(\Rightarrow SH=AH.tan60^0=\dfrac{AB.BC.AC.\sqrt{3}}{4S_{ABC}}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{AB.BC.CA.\sqrt{3}}{4S_{ABC}}.S_{ABC}=\dfrac{5a^3\sqrt{3}}{12}\)
Đúng 1
Bình luận (0)
Cho hình chóp tam giác đều
S
.
A
B
C
có độ dài cạnh đáy bằng a, góc hợp bởi cạnh bên và mặt đáy bằng
60
∘
.Tính thể tích khối chóp đã cho. A.
3
a
3
12
B.
3
a
3
6
C. ...
Đọc tiếp
Cho hình chóp tam giác đều S . A B C có độ dài cạnh đáy bằng a, góc hợp bởi cạnh bên và mặt đáy bằng 60 ∘ .Tính thể tích khối chóp đã cho.
A. 3 a 3 12
B. 3 a 3 6
C. 3 a 3 3
D. 3 a 3 4
Đáp án A
Gọi H là hình chiếu của S lên lên (ABCD).

A H = 2 3 a 2 - a 2 2 = a 3 3 S H = A H tan 60 ∘ = a 3 3 . 3 = a
Thể tích khối chóp là:
V = 1 3 S A B C · S H = 1 3 · 1 2 a 2 sin 60 ° . a = a 3 . 3 12
Đúng 0
Bình luận (0)