Vì SABC là hình chóp đều nên nó sẽ có tính đối xừng, và cách làm giống bài bên trên toi vừa làm, bạn tham khảo
Cho hình chóp đều SABCD. Cạnh đáy bằng a góc giữa cạnh bên và đáy bằng 30°. Tính khoảng cách từ a)B đến (SAC) b)O đến (SCD) c)AB đến (SCD)
Cho hình chóp đều SABC cạnh đáy bằng a. Tâm O góc giữa (SBC) và đáy bằng 60°. Tính khoảng cách từ a)O đến (SAB) b)C đến (SAB)
Cho hình chóp SABCD đều. Cạnh đáy a, góc giữa mặt bên và đáy bằng 45°. Tính khoảng cách từ a)A đến (SBD) b)O đến (SAB) c)CD đến (SAB)
Cho hình chóp đều SABC tâm O cạnh đáy bằng a cạnh bên SA = 3a tính khoảng cách từ E đến mặt phẳng SBC với E là trung điểm của SA
Cho hình chóp SABCD đáy là hình thoi tâm O cạnh a. (SAD) và (SAC) cùng vuông góc với đáy. Góc BAD=120°, SA=a căn 2. Tính khoảng cách từ a)SB đến CD b)BD đến SC c)SC đến AB
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng 60 0 . Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
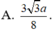
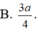
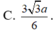
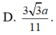
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là 60 o . Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
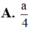
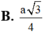
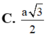
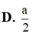
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3 . Gọi O là tâm đáy ABC, d 1 là khoảng cách từ A đến mặt phẳng (SBC) và d 2 là khoảng cách từ O đến mặt phẳng (SBC). Tính d = d 1 + d 2
A. d = 2 a 2 11
B. d = 2 a 2 33
C. d = 8 a 22 33
D. d = 8 a 2 11
