Tìm GTLN, GTNN của hàm số y = 3- cos2x - 3sinx.

Những câu hỏi liên quan
Tìm GTLN, GTNN của hàm số : y= -2sin2x + 3sinx -1
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=-2t^2+3t-1\)
\(\Rightarrow y_{min}=min\left\{f\left(-1\right);f\left(1\right);f\left(\dfrac{3}{4}\right)\right\}=f\left(-1\right)=-6\)
\(y_{max}=max\left\{f\left(-1\right);f\left(1\right);f\left(\dfrac{3}{4}\right)\right\}=f\left(\dfrac{3}{4}\right)=\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
Tìm GTLN và GTNN của hàm số
y=3sinx + 4cosx + 5
A. min y = 0, max y= 13
B. min y =0, max y=10
C. min y= 1, max y=10
D. Tất cả sai
Tìm GTLN, GTNN của hàm số y = -2sin2x +3sinx -1
tìm gtln gtnn của hàm số y=|sinx +cos2x|-2sinx
\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
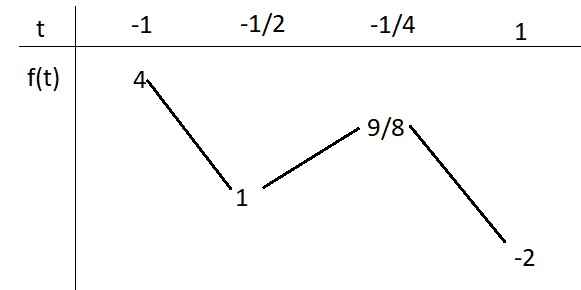
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)
Đúng 1
Bình luận (0)
Tìm GTLN và GTNN của hàm số: y = |sinx + cos2x|
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)
Đúng 0
Bình luận (0)
Tìm GTLN; GTNN của các hàm số
\(a,y=3-4sin^2xcos^2x\)
\(b,y=\dfrac{-2}{3sinx-5}\) trên đoạn \(\left[0;\dfrac{\pi}{2}\right]\)
a, \(y=3-4sin^2x.cos^2x=3-sin^22x\)
Đặt \(sin2x=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=3-t^2\)
\(\Rightarrow y_{min}=minf\left(t\right)=2\)
\(y_{max}=maxf\left(t\right)=3\)
Đúng 1
Bình luận (0)
b, \(y=f\left(t\right)=\dfrac{-2}{3t-5}\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y_{min}=minf\left(t\right)=\dfrac{2}{5}\)
\(y_{max}=maxf\left(t\right)=1\)
Đúng 1
Bình luận (0)
Tìm GTLN, GTNN của hàm số :
\(y=sin^3x-cos2x+sinx-1\)
\(y=sin^3x+2sin^2x+sinx-2\)
đặt \(t=sinx\) với \(t\in\left[-1;1\right]\)
pt \(\Leftrightarrow\)\(y=t^3+2t^2+t-2\)
\(y'=3t^2+4t+1\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{3}\end{matrix}\right.\)
| x | -1 -1/3 1 |
| y' | 0 - 0 + |
| y | -2 - -58/27 + 2 |
vậy GTLN của y = 2 với t=1 \(\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
GTNN của y=-58/27 với \(t=-\dfrac{1}{3}\Leftrightarrow sinx=-\dfrac{1}{3}\Leftrightarrow x=sin^{-1}\left(-\dfrac{1}{3}\right)\)
Đúng 1
Bình luận (0)
1/ Xét tính chẵn lẻ của hàm số: y = f(x) = căn (2-sin3x) - căn(2+sin3x) 2/ Tìm GTLN-GTNN của hàm số sau: y = f(x)= cos2x + 3 sin2sin2x - 2
Tìm GTLN; GTNN của các hàm số:
\(a,y=2sin^2x-cos2x\)
\(b,y=3\sqrt{1+sinx}-1\) trên đoạn \(\left[0;\dfrac{\pi}{3}\right]\)
a, \(y=2sin^2x-cos2x=1-2cos2x\)
Vì \(cos2x\in\left[-1;1\right]\Rightarrow y=2sin^2x-cos2x\in\left[-1;3\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=-1\\y_{max}=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
















