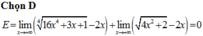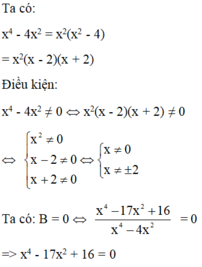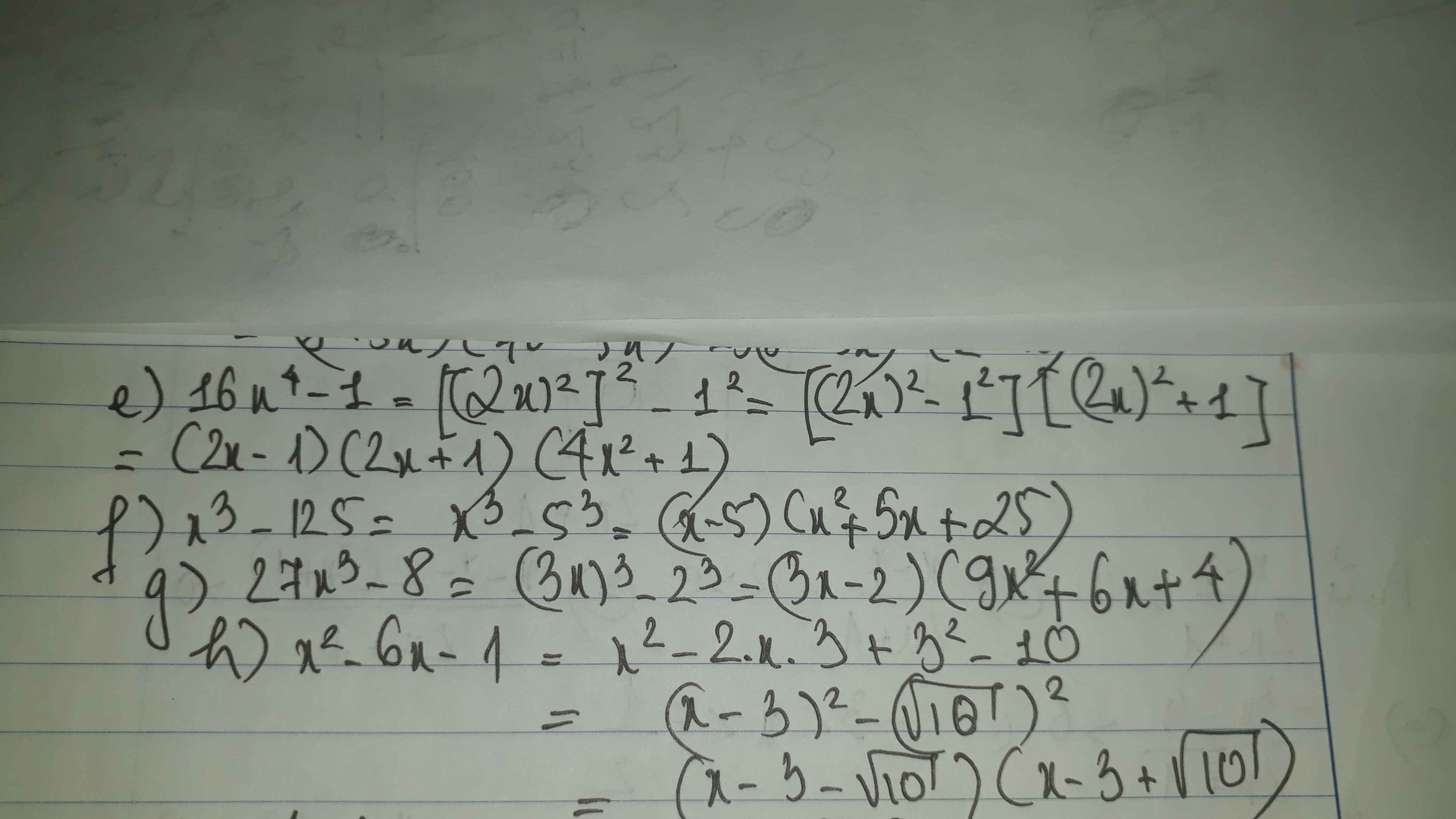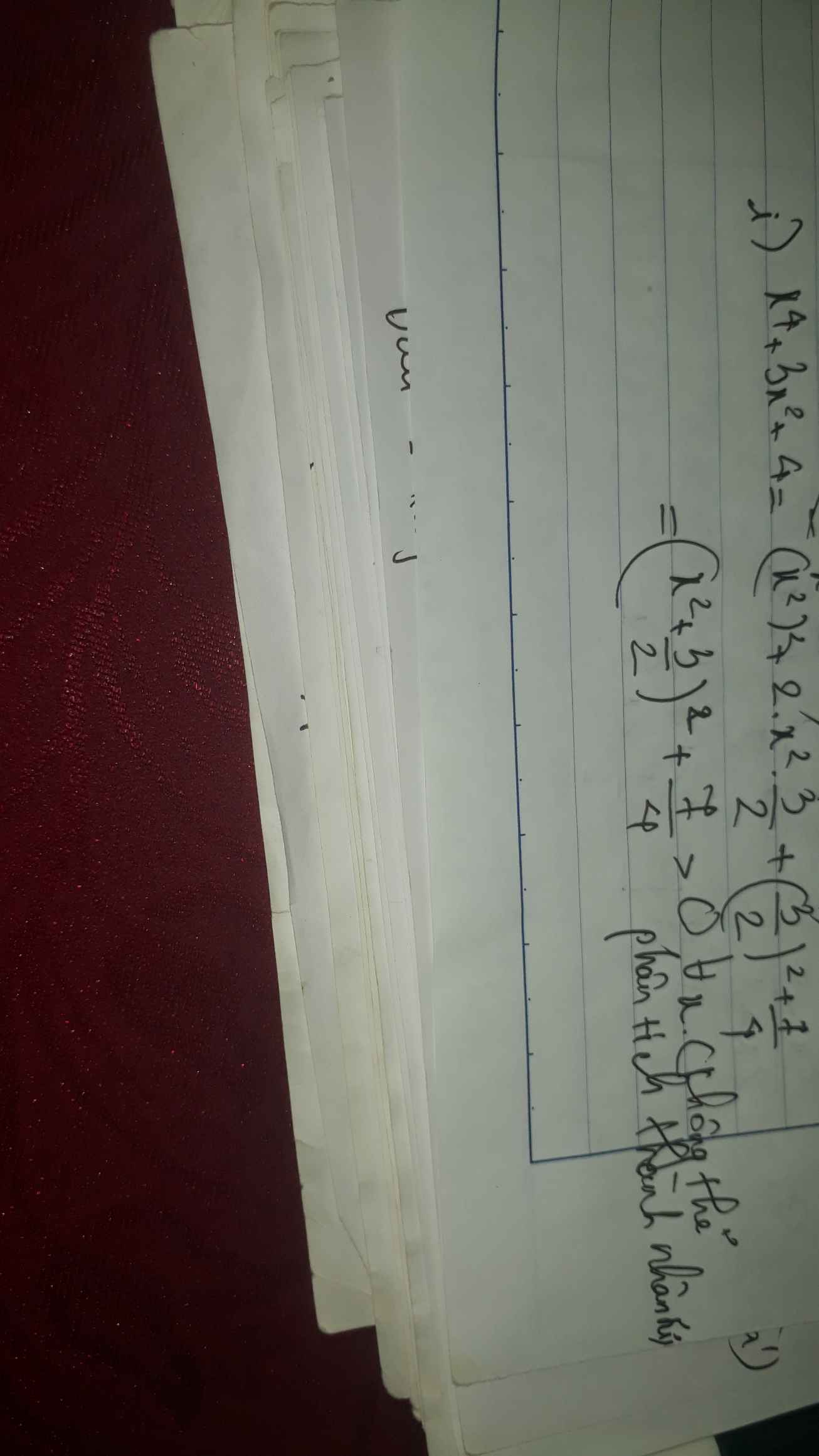(4x^2-7x-50)^2-16x^4-56x^3-49x^2

Những câu hỏi liên quan
Câu I (1,5 điểm) Thực hiện phép tính:
a)2x2(3x2 – 7x – 5)
b) (16x4 - 20x2y3 - 4x5y) : (-4x2)
a) Ta có: \(2x^2\left(3x^2-7x-5\right)\)
\(=2x^2\cdot3x^2-2x^2\cdot7x-2x^2\cdot5\)
\(=6x^4-14x^3-10x^2\)
c) Ta có: \(\left(16x^4-20x^2y^3-4x^5y\right):\left(-4x^2\right)\)
\(=16x^4:\left(-4x^2\right)+20x^2y^3:4x^2+4x^5y:4x^2\)
\(=-4x^3+5y^3+x^3y\)
Đúng 0
Bình luận (0)
tính bằng cách thuận tiện
a. 49x8+49x2
b. 123x45+123x55
c. 72x2+72x3+72x5
d. 56x4+56x3+56x2+56x1
a.49x8+49x2=49x(8+2)
=49x10
=490
Các câu khác làm tương tự
Tìm giới hạn
E
lim
x
→
+
∞
16
x
4
+
3
x
+
1
4...
Đọc tiếp
Tìm giới hạn E = lim x → + ∞ 16 x 4 + 3 x + 1 4 - 4 x 2 + 2 .
![]()
![]()
![]()
![]()
a) 6x3:(-3x2)
b) (-9x2):6x
c) (-16x4):(-12x3)
d) (8x3+4x2-6x):2x
a) 6x³ : (-3x²) = [6 : (-3)] . (x³ : x²)
= -2x
b) (-9x²) : 6x
= (-9 : 6) . (x² : x)
= -3/2 x
c) (-16x⁴) : (-12x³)
= [-16 : (-12)] . (x⁴ : x³)
= 4/3 x
d) (8x³ + 4x² - 6x) : 2x
= 8x³ : 2x + 4x² : 2x - 6x : 2x
= 4x² + 2x - 3
Đúng 3
Bình luận (0)
1)7x^2-49x
2)8x^2-16x
3)2x^3+40x
4)-x^3+16x
1)
`7x^2 -49x=0`
`<=>x(7x-49)=0`
\(< =>\left[{}\begin{matrix}x=0\\7x-49=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
2)
`8x^2 -16x=0`
`<=>x(8x-16)=0`
\(< =>\left[{}\begin{matrix}x=0\\8x-16=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
3)
`2x^3 +40x=0`
`<=>x(2x^2 +40)=0`
`<=>x=0` hoặc`2x^2 +40=0`
`<=>x=0` hoặc `2x^2 =-40` (vô lí vì `2x^2` luôn lớn hơn hoặc bằng 0)
`<=>x=0`
4)
`-x^3 +16x=0`
`<=>x^3 -16x=0`
`<=>x(x^2 -16)=0`
\(< =>\left[{}\begin{matrix}x=0\\x^2-16=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho B
x
4
−
17x
2
+
16
x
4
−
4x
2
. Có bao nhiêu giá trị của x để B 0. A. 2 B. 3 C. 1 D. 4
Đọc tiếp
Cho B = x 4 − 17x 2 + 16 x 4 − 4x 2 . Có bao nhiêu giá trị của x để B = 0.
A. 2
B. 3
C. 1
D. 4
(49x2-y2):(7x-y)
\(=\dfrac{\left(7x-y\right)\left(7x+y\right)}{7x-y}=7x+y\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm
x
∈
[
1
;
2
]
.
x
4
+
16
x
4
+
4
(
x
2
+
4
x
2
)
-
12
(
x
-
2
x
)
m
A.
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x ∈ [ 1 ; 2 ] .
x 4 + 16 x 4 + 4 ( x 2 + 4 x 2 ) - 12 ( x - 2 x ) = m
A. - 13 ≤ m ≤ 11
B. - 15 ≤ m ≤ 9
C. - 15 < m < 9
D. - 16 ≤ m ≤ 9
Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
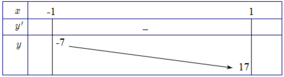
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 16x2+24x+9
b) -36a2b2+12ab-1
c) (3-7x)2-2(3-7x)(x-2)2+4-4x+x2
d) 81-(25x2-10x+1)
e) 16x4-1
f) x3-125
g) 27x3-8
h) x2-6x-1
i) x4+3x2+4
4x2 - 7x + 2 = 0 ?????
\(\left[{}\begin{matrix}x=\dfrac{7-\sqrt{17}}{8}\\x=\dfrac{7+\sqrt{17}}{8}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(\Leftrightarrow\left(x-2\right)\left(4x+1\right)=0\)
\(\Leftrightarrow x-2=0\) hay \(4x+1=0\)
\(\Leftrightarrow x=2\) \(\Leftrightarrow\) \(4x=-1\)
\(\Leftrightarrow x=-\dfrac{1}{4}\)
Vậy \(S=\left\{2,-\dfrac{1}{4}\right\}\)
Đúng 1
Bình luận (0)
\(\Delta=\left(-7\right)^2-4\cdot4\cdot2=49-32=17\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7-\sqrt{17}}{8}\\x_2=\dfrac{7+\sqrt{17}}{8}\end{matrix}\right.\)
Đúng 1
Bình luận (0)